-> А - да, В - нет
А - да, В - да
А - нет, В - да
А - нет, В - нет
Даны два вектора 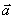 (1, -2, 4) и
(1, -2, 4) и 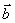 (6, 1, 4)
(6, 1, 4)
-> эти векторы лежат в одной плоскости
эти векторы коллинеарны
эти векторы ортогональны
эти векторы линейно зависимы
Даны четыре пары векторов 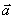 и
и 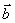 Расположите эти пары векторов по возрастанию их скалярных произведений. А)
Расположите эти пары векторов по возрастанию их скалярных произведений. А) 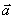 (2,1,1),
(2,1,1), 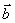 (3, -2. 0); В)
(3, -2. 0); В) 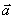 (0,-1,1),
(0,-1,1), 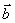 (2, -2. 0); C)
(2, -2. 0); C) 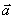 (3,-1,1),
(3,-1,1), 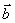 (3, -2. 0); D)
(3, -2. 0); D) 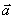 (4,1,-1),
(4,1,-1), 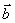 (1, 2. 0)
(1, 2. 0)
-> B)  = 2
= 2
-> A)  = 4
= 4
-> D)  = 6
= 6
-> C)  = 11
= 11
Дана теорема: пусть 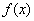 задана на
задана на 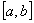 и удовлетворяет двум условиям: 1)
и удовлетворяет двум условиям: 1) 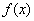 непрерывна на
непрерывна на 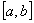 ; 2)
; 2) 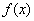 имеет производную
имеет производную 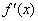 в
в 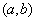 . Тогда внутри
. Тогда внутри 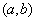 найдется по крайней мере одна такая точка с, что
найдется по крайней мере одна такая точка с, что 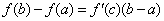 . Эта теорема носит имя ___________
. Эта теорема носит имя ___________
-> Лагранжа
Установить соответствие между строками в столбцах ниже
-> собственный базис матрицы 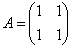 может состоять из векторов <->
может состоять из векторов <-> 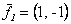 ,
, 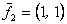
-> собственный базис матрицы 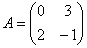 может состоять из векторов <->
может состоять из векторов <-> 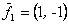 ,
, 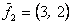
-> вектор 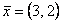 является собственным для матрицы
является собственным для матрицы 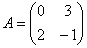 , отвечающим собственному значению <->
, отвечающим собственному значению <-> 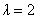
-> вектор 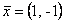 является собственным для матрицы
является собственным для матрицы 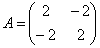 и отвечает собственному значению <->
и отвечает собственному значению <-> 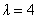
Базис, состоящий из единичных по длине, взаимно ортогональных векторов, называется __________
-> ортонормированным
Уравнение 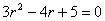 является характеристическим для однородных дифференциальных уравнений, соответствующих нижеприведенным неоднородным
является характеристическим для однородных дифференциальных уравнений, соответствующих нижеприведенным неоднородным
-> 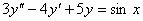
-> 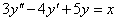
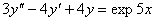
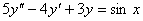
Подберите правильный ответ
|
|

Сейчас читают про:
 2015-05-20
2015-05-20 424
424







