Дифференциальные уравнения первого порядка
А. Уравнения с разделяющимися переменными
1. 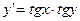 2.
2. 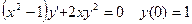 3. ylnydx+xdx=0
3. ylnydx+xdx=0
4. y’ctgx+y=2 5. 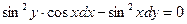 6.
6. 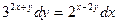
7. 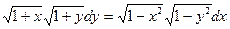
Б. Линейные уравнения
8. y/sinx-y cosx =1, 9. y/-y sinx=e-cosxsin2x
10. y/cosx - 2y sinx=2 11. y/x lnx – y=3x3ln2x,
12. 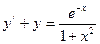 13.
13. 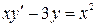
14. 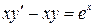 15.
15. 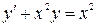
16. 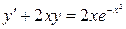 17.
17. 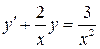
18. 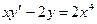 19.
19. 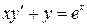
20. 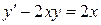 21.
21. 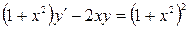
22. 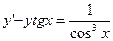 23.
23. 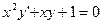
24. 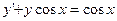 25.
25. 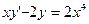
26. 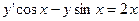 27.
27. 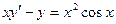
28. 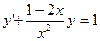 29.
29. 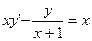
30. 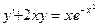 31.
31. 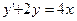
33. 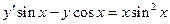 34.
34. 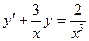
35. 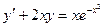 36.
36. 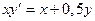 .
.
Найти решение задачи Коши:
37. xy|-3y=x4ex y0=e x0=1 38. 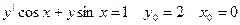
39. 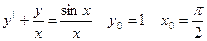 40.
40. 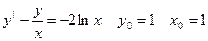
41. 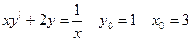 42.
42. 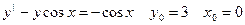
43. 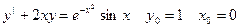 44.
44. 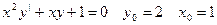
45. 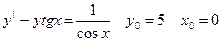 46.
46. 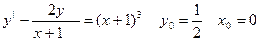
В. Однородные уравнения
47. (x-y)dx+xdy=0; 48. x2dy=(y2-xy+x2)dx
49. 2x2y/=x2+y2 50. 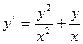
51. xy/=y(lny - lnx) 52. 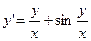
53. 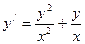 54.
54. 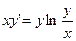
55. 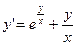 56.
56. 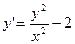
Дифференциальные уравнения второго порядка
А. Линейные дифференциальные уравнения второго порядка со специальной правой частью
57. 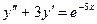 58.
58. 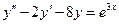
59. 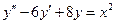 . 60.
. 60. 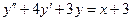
61. 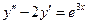 . 62.
. 62. 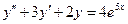
63. 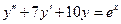 . 64.
. 64. 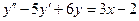
65. 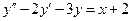 . 66.
. 66. 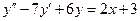
67. 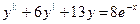 68.
68. 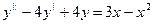
69. 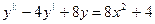 70.
70. 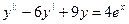
71. 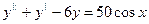 72.
72. 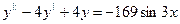
73. 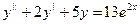 74.
74. 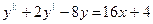
75. 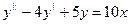 76.
76. 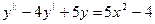
77. y”+y’-2y = 8 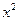 -4x 78. y”-3y’ = 18
-4x 78. y”-3y’ = 18 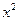 -2
-2
79. y”+2y’+y = 4 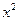 -3x-5 80. y”-4y’+3y = 8
-3x-5 80. y”-4y’+3y = 8 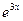
81. y”-2y’-2y =12x 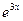 82. y”-2y’+y = 10
82. y”-2y’+y = 10 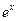
83. y”+y = cos3x 84. y”+4y = cos2x
85. y”+5y’+6y = -50sin4x 86. y”-2y’+2y = 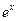 sinx
sinx
Найти решение задачи Коши:
87. 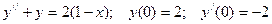
88. 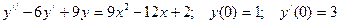
89. 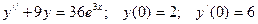
90. 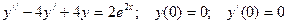
91. 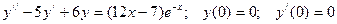
92. 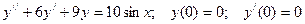
93. 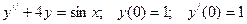
94. 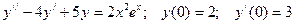
95. 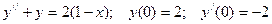
96. 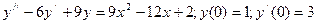
97. 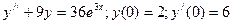
98. 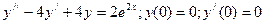
99. 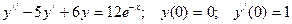
100. 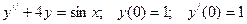
Б. Уравнения, допускающие понижение порядка
101. 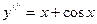 102.
102. 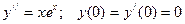
103. 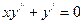 104.
104. 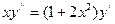
105. 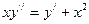 106.
106. 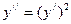
107. 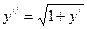 108.
108. 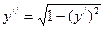
109. 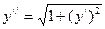 110.
110. 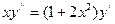
111. 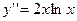 112.
112. 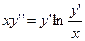
113. 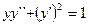 114.
114. 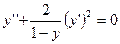
Решить систему дифференциальных уравнений.
115. 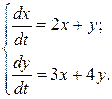
116. 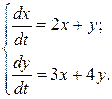
КРАТНЫЕ ИНТЕГРАЛЫ
 2015-05-20
2015-05-20 829
829








