2015-05-20
861
Законы теплового излучения играют важную роль в различных сферах человеческой деятельности. Так, на сберегающих лампах часто указывают цветовую температуру (спектрофотометрическую или колориметрическую температуру — Т с), соответствующую температуре равновесного излучения спектра данной лампы. Равновесное излучение используется для определения температуры тел по их спектру изучения. Важно отметить, что в этом случае возможно определить, в частности, температуру удалённых и сильно нагретых тел. Использование теплового излучения играет неоценимую роль при разработке приборов ночного видения и т.п.
Открытие и изучение законов равновесного излучения послужило первым шагом в осознании корпускулярно-волнового дуализма квантовых объектов и сыграло решающую роль в создании квантовой механики. Поэтому представляется важным ознакомить студентов не только с теоретическим описанием законов теплового излучения, но и с изучением этих законов в лабораторных условиях.
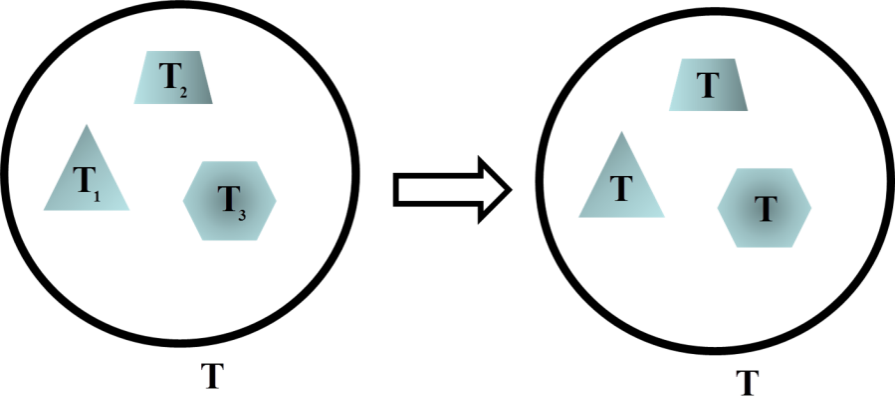
Рис. 1. Схематическое изображение процесса установления термодинамического равновесия (выравнивания температур) за счёт излучения (температура стенок полости поддерживается постоянной): слева — тела в вакууме в начальный момент времени; справа — после установления теплового равновесия
Перед обсуждением свойств равновесного электромагнитного излучения рассмотрим одно из явлений, где это излучение проявляется наиболее явно, — замкнутую полость, стенки которой поддерживаются при постоянной температуре T, а внутри полости находятся тела, имеющие различные температуры T 1, T 2, T 3 (рис. 1). Воздух из полости откачан, а тела внутри вакуумной полости не соприкасаются. Установлено, что спустя некоторое время температура всех тел становится одинаковой и равной температуре стенок.
Поскольку внутри полости вакуум, то средой, являющейся переносчиком тепла между телами и стенками полости, является электромагнитное поле. Экспериментально установлено, что в состоянии теплового равновесия свойства излучения не зависят ни от формы, ни от материала тел и стенок полости. Излучение, образуемое в полости после установления теплового равновесия, называется равновесным или тепловым. Его свойства можно изучать, проделав в оболочке маленькое (площадью много меньше, чем площадь всей оболочки) отверстие и расположив прямо напротив него детектор (рис. 2).
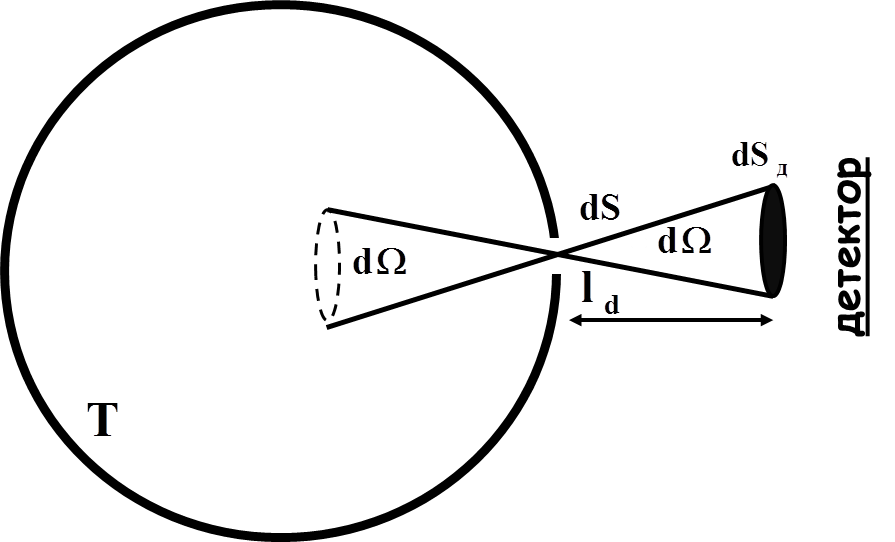
Рис. 2. Схема эксперимента по изучению свойств теплового излучения
Рассмотрим характеристики, используемые для описания свойств равновесного излучения. Это позволит понять, что должен регистрировать детектор. Отметим, что эти же характеристики имеют смысл и для неравновесного излучения.
1. Плотность энергии (энергия в единице объёма) излучения зависит только от температуры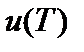 
и может быть представлена в виде:
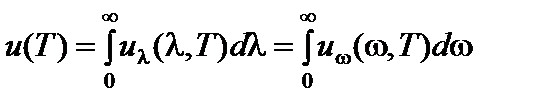. (1)
Величины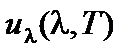 
и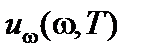 
называются спектральными плотностями лучистой энергии и имеют смысл объёмной плотности энергии, приходящейся на интервал длин волн 
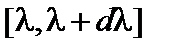или на интервал частот 
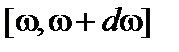, соответственно.
2. Удельная интенсивность излучения I (T). Она позволяет вычислить поток энергии dW, который проходит через площадку dS в направлении нормали к этой площадке в пределах телесного угла dΩ за время dt:
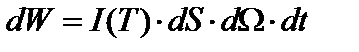. (2)
Этот поток будет зарегистрирована детектором (рис. 2). Если излучение падает под углом q по отношению к нормали к площадке, то:
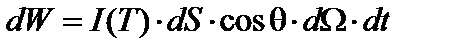. (2a)
Спектральные разложения удельной интенсивности излучения представимы в следующей форме:
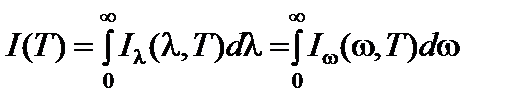. (3)
Спектральные плотности энергии и удельные интенсивности излучения связаны соотношениями:
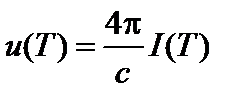(4)
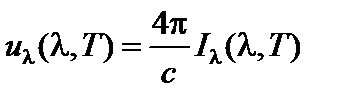(4a)
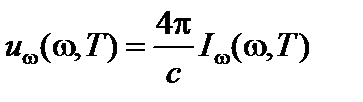, (4b)
которые получены в предположении, что излучение любой длины волны (частоты) распространяется в вакууме изотропно со скоростью света c. Частота и длина волны излучения связаны соотношением
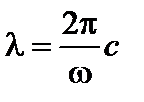. (5)
Интенсивности излучения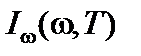 
и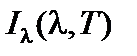 
связаны интегральным соотношением
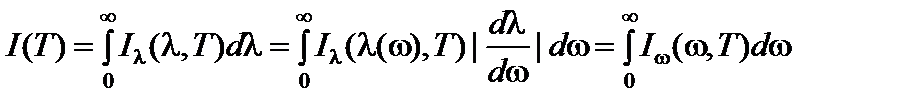. (6)
Для подынтегральных функций справедливы выражения:
; 
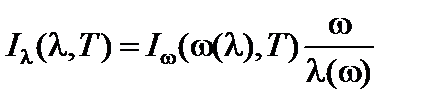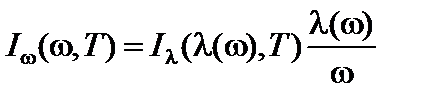. (7)
Условие равенства излученной и поглощённой энергии телами системы, находящимися в состоянии термодинамического равновесия, накладывает жесткие ограничения на способность тел поглощать и испускать электромагнитное излучение. Поток лучистой энергии, излучаемый в интервал частот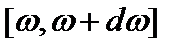 
за время dt площадкой dS внутрь полости можно записать в виде:
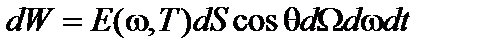, (8)
где q — угол между направлением испускания излучения и нормалью к площадке dS. Множитель cosq учитывает «видимую» (перпендикулярную к направлению излучения) площадь, с которой происходит излучение (рис. 3). Величина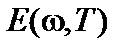 
называется излучательной способностью тела.
Поглощательной способностью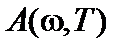 
тела называется величина, равная доле падающего излучения, которая поглощается поверхностью. Это значит, что 
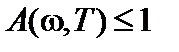. Коэффициент отражения равен 
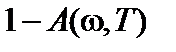. Если между стенками полости и излучением установилось термодинамическое равновесие, то энергия, переданная излучением стенкам и полученная от стенок равны. В противном случае стенки нагревались бы или остывали.
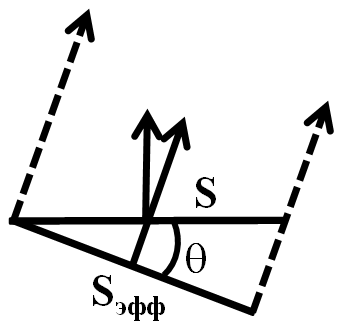
Рис. 3. Влияние ориентации излучающей поверхности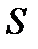 
на её эффективную площадь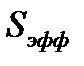 
Требование баланса энергии (или закона сохранения энергии) приводит к соотношению, связывающему удельную интенсивность излучения с поглощательной и излучательной способностями. Рассмотрим случай, когда тело (стенка) поглощает всю падающую лучистую энергию, тогда
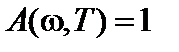. (9)
Такое тело называется абсолютно черным. Естественно задать вопрос: какой излучательной способностью обладает абсолютно черное тело? Формула (8) определяет количество энергии, излучаемой площадкой за рассматриваемый интервал времени, в заданный интервал углов и частот. Формула (2а) определяет энергию, падающую за время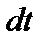 
в заданный телесный угол 
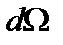на ту же площадку в интервале частот 
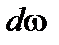. В условиях термодинамического равновесия эти энергии должны быть равны:
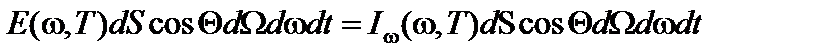. (10)
Это равенство означает, что излучательная способность абсолютно черного тела равна удельной интенсивности равновесного излучения:
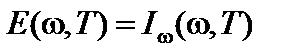. (11)
Если тело не является абсолютно черным, то к излученной энергии добавляется отраженная энергия, которую необходимо учесть в левой части выражения (10). Поскольку падающая энергия равна
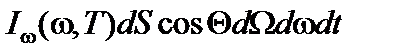, (12)
то отраженная энергия зависит от коэффициента отражения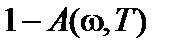 
и определяется следующим выражением
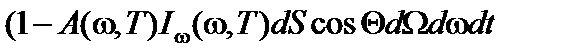. (13)
Уравнение баланса падающей и излучаемой энергии (10) с учетом отражения запишется в виде:
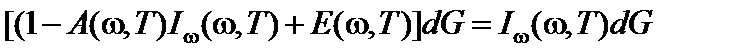. (13)
Здесь введено обозначение 
. Это приводит к связи между излучательной и поглощательной способностями:
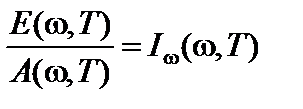. (14)
Это выражение называется законом Кирхгофа и формулируется следующим образом: отношение излучательной способности тела к его поглощающей способности одинаково для всех тел и является универсальной функцией только частоты и температуры.
Выражение для удельной интенсивности излучения было получено Максом Планком. Оно имеет следующий вид:
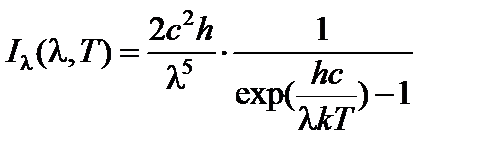, (15)
где,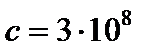 
м/с — скорость света в вакууме; 
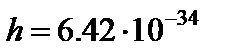Дж 
с — постоянная Планка, 
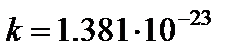Дж/K — постоянная Больцмана.
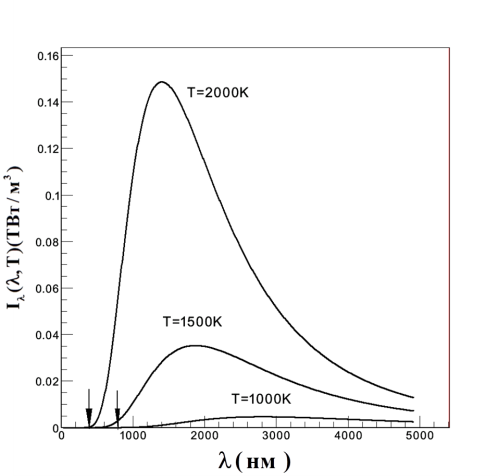
Зависимость удельной интенсивности излучения от длины волны для различных температур показана на рис. 4.
Рис. 4. Зависимость удельной интенсивности равновесного излучения от длины волны для различных температур (стрелками показан интервал длины волн, соответствующий области видимого света)
Из рис. 4 видно, что при низких температурах излучение сосредоточено в области больших длин волн. C ростом температуры максимум излучения смещается в область более коротких длин волн. Как следует из (15), наряду с изменением интервала, в котором сосредоточено излучение, растёт также и величина удельной интенсивности излучения.
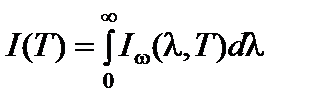. (16)
Для работы с уравнением (15) удобно ввести безразмерную переменную
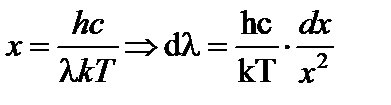. (17)
Тогда удельная интенсивность излучения запишется следующим виде:
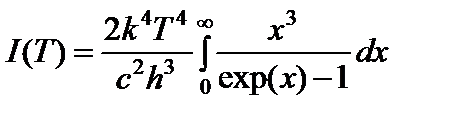. (18)
Видно, что она пропорциональна четвёртой степени температуры. Определенный интеграл равен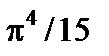 
. Тогда для удельной интенсивности излучения получим:
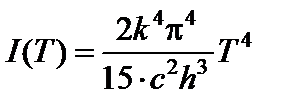. (19)
Используя выражение (19), найдем энергию, которая будет попадать в детектор в единицу времени:
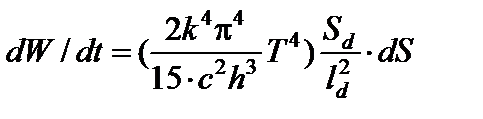. (20)
Здесь Sd — площадь детектора,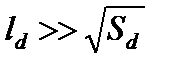 
— расстояние от отверстия до детектора и dS — площадь отверстия. Для описания интенсивности изучения абсолютно чёрного тела вводится величина, называемая интегральной энергетической светимостью — R. Она определяется количеством энергии, излучаемой с единичной поверхности за единицу времени в интервале частот от 0 до ∞ при данной температуре Т с учётом изменения «видимого» размера изучающей площадки dS, зависящей от направления излучения q(рис. 3).
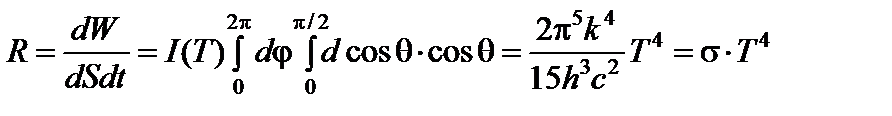. (21)
Закон, согласно которому энергетическая светимость абсолютно черного тела растёт пропорционально четвёртой степени температуры, называется законом Стефана-Больцмана. Коэффициент пропорциональности s называется постоянной Стефана-Больцмана и равен:
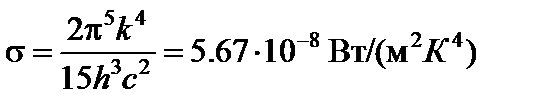. (22)
