Определение. Функция f*(x1,..., xn) называется двойственной к функции f(x1,..., xn), если f*(x1,..., xn) = 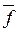 (
(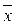 1,...,
1,..., 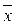 n).
n).
Пример 8. Покажем с помощью таблицы истинности (табл. 13), что константа 0 двойственна к 1.
Таблица 13
| x | f | f * |
Функции f (x) = x и g (x) = 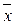 двойственны сами себе (табл. 14).
двойственны сами себе (табл. 14).
Таблица 14
| x | f | f * | g | g * |
Определение. Если f*(x1,..., xn) = f(x1,..., xn), то f(x1,..., xn) называется самодвойственной.
Если f *– самодвойственна, то 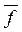 (
(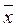 1,...,
1,..., 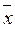 n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
Пример 9. Покажем, что f (x 1, x 2, x 3)= x 1Å x 2Å x 3 – самодвойственна (табл. 15).
Таблица 15
| x 1 | x 2 | x 3 | f | f * |
Пример 10. Покажем, что функция x1&x2 двойственна к х1Úх2, функция х1 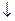 х2 двойственна к функции x1|x2 (табл. 16).
х2 двойственна к функции x1|x2 (табл. 16).
Таблица 16
| x 1 x 2 | f = х 1Ú х 2 | f * | g = x 1| x 2 | g *= x 1 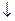 x 2 x 2
|
| 0 0 0 1 1 0 1 1 |
Теорема о двойственных функциях.
Если f * двойственна к f, то f двойственна к f *.
Доказательство. f *(x 1,..., xn) = 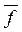 (
(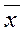 1,...,
1,..., 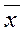 n). Найдем двойственную функцию к f *, т.е. (f *(x 1,..., xn))* = (
n). Найдем двойственную функцию к f *, т.е. (f *(x 1,..., xn))* = (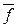 (
(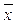 1,...,
1,..., 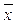 n))* =
n))* =
= 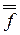 (
(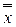 1,...,
1,..., 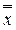 n) = f (x 1,.., xn).
n) = f (x 1,.., xn).
Предположим, что функция задана формулой. Можно ли найти по этой формуле двойственную функцию? Ответ на этот вопрос дает следующая теорема.
 2015-05-20
2015-05-20 364
364








