Дадим индуктивное определение формулы над множеством. Это определение несколько сложное по форме, но будет полезно в дальнейшем. С индуктивным определением мы встречались в математическом анализе при определении 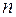 -го дифференциала
-го дифференциала 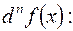 было введено понятие первого дифференциала
было введено понятие первого дифференциала 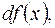 а затем
а затем 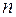 -й дифференциал определялся как первый дифференциал от
-й дифференциал определялся как первый дифференциал от 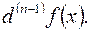
Определение. Пусть 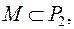 тогда:
тогда:
1) каждая функция 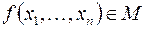 называется формулой над
называется формулой над 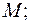
2) пусть 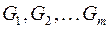 – либо переменные, либо формулы над
– либо переменные, либо формулы над 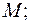
3) если 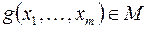 , то
, то 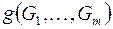 – называется формулой над
– называется формулой над 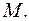
Формулы будем обозначать заглавными буквами: 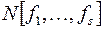 , имея в виду функции, участвовавшие в построении формулы, или
, имея в виду функции, участвовавшие в построении формулы, или 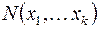 имея в виду переменные, вошедшие в формулу.
имея в виду переменные, вошедшие в формулу.
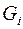 – формулы, участвовавшие в построении
– формулы, участвовавшие в построении 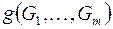 , называются подформулами.
, называются подформулами.
Пример 5. Пусть 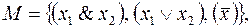 тогда
тогда 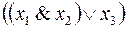 – формула над
– формула над 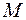 .
.
Сопоставим каждой формуле 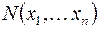 функцию
функцию 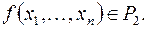 Сопоставление будем производить в соответствии с индуктивным определением формулы.
Сопоставление будем производить в соответствии с индуктивным определением формулы.
1) Пусть 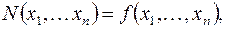 тогда формуле
тогда формуле 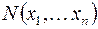 сопоставим функцию
сопоставим функцию 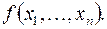
2) Пусть 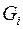 – формула над
– формула над 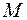 и пусть ей по индуктивному предположению сопоставлена функция
и пусть ей по индуктивному предположению сопоставлена функция 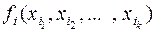 . Если
. Если 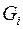 – переменная, то есть
– переменная, то есть 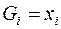 , то ей сопоставим функцию
, то ей сопоставим функцию 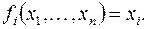
Таким образом, каждой подформуле 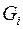 сопоставлена функция
сопоставлена функция 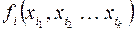 , где каждая функция зависит от своих переменных и их число может быть различным. Но
, где каждая функция зависит от своих переменных и их число может быть различным. Но 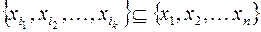
переменных, перечисленных в формуле 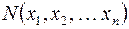 . В каждую функцию
. В каждую функцию 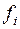 введем недостающие переменные (они будут фиктивными), получим, что каждой подформуле
введем недостающие переменные (они будут фиктивными), получим, что каждой подформуле 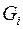 сопоставлена функция
сопоставлена функция 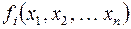 .
.
3) Тогда
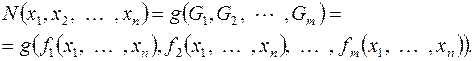
Сопоставим формуле 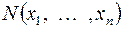 функцию
функцию 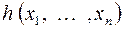 следующим образом: пусть
следующим образом: пусть 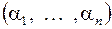 – произвольный набор переменных, пусть
– произвольный набор переменных, пусть 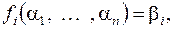 тогда
тогда 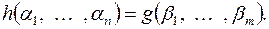
Множество всех формул над M обозначим через < M >.
Определение. Две формулы N и D из <M> называются равными N=D или эквивалентными N~D, если функции, реализуемые ими, равны.
Упрощение записи формул:
1) внешние скобки можно опускать;
2) приоритет применения связок возрастает в следующем порядке: ~, 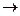 , Ú, &;
, Ú, &;
3) связка  над одной переменной сильнее всех связок;
над одной переменной сильнее всех связок;
4) если связка  стоит над формулой, то сначала выполняется формула, затем отрицание;
стоит над формулой, то сначала выполняется формула, затем отрицание;
5) если нет скобок, то операции ~ и 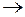 выполняются в последнюю очередь.
выполняются в последнюю очередь.
Пример 6. Доказать эквивалентность формул (табл. 11).
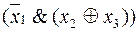 ~ (
~ (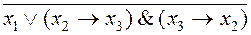 ).
).
Таблица 11
| x 1 | x 2 | x 3 | x 2Å x 3 | & 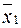
| x 2 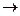 x 3 x 3
| x 3 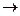 x 2 x 2
| & | Ú x 1 | – |
 2015-05-20
2015-05-20 448
448








