Определение. Система функций {f1, f2,..., fs,...} 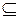 P2 называется полной в Р2, если любая функция f(x1,..., xn) Î P2 может быть записана в виде формулы через функции этой системы.
P2 называется полной в Р2, если любая функция f(x1,..., xn) Î P2 может быть записана в виде формулы через функции этой системы.
Полными системами, например, являются само 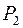 или множество
или множество 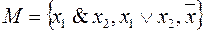 , так как каждая функция может быть представлена в виде СДНФ или СКНФ, где используются только эти связки. Примерами неполных систем являются
, так как каждая функция может быть представлена в виде СДНФ или СКНФ, где используются только эти связки. Примерами неполных систем являются 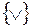 или
или 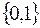 .
.
Лемма (достаточное условие полноты).
Пусть система  U = { f 1, f 2,..., fs,...} полна в Р 2,
U = { f 1, f 2,..., fs,...} полна в Р 2, 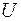 – диагностическая система. Пусть B = { g 1, g 2,..., gk,...} – некоторая система из Р 2, причем любая функция fi Î U может быть выражена формулой над B, тогда система B полна в Р 2.
– диагностическая система. Пусть B = { g 1, g 2,..., gk,...} – некоторая система из Р 2, причем любая функция fi Î U может быть выражена формулой над B, тогда система B полна в Р 2.
Доказательство. Пусть h(x1,..., xn) Î P2; так как U полна в Р2, то h(x1,..., xn) =N[f1,..., fs,...] = N[L1[g1,..., gk,...],..., Ls[g1,..., gk,...],...] = = 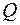 [g1,..., gk]. Здесь мы воспользовались тем, что для любого i
[g1,..., gk]. Здесь мы воспользовались тем, что для любого i 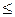 n fi может быть выражена формулой над B, поэтому fi=Li[gi,..., gk,...].
n fi может быть выражена формулой над B, поэтому fi=Li[gi,..., gk,...].
С помощью леммы докажем полноту некоторых важных систем.
1. Система 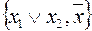 полна в
полна в 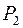 .
.
Возьмем в качестве полной в Р 2 системы U ={ x 1Ú x 2, 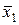 , x 1& x 2}, B ={ x 1Ú x 2,
, x 1& x 2}, B ={ x 1Ú x 2, 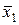 }. Надо показать, что x 1& x 2 представляется формулой над B. Действительно, по правилу Де Моргана получим x 1& x 2=
}. Надо показать, что x 1& x 2 представляется формулой над B. Действительно, по правилу Де Моргана получим x 1& x 2= 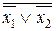 .
.
2. Система { x 1& x 2, 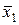 } – полна в Р 2.
} – полна в Р 2. 
3. Система { x 1| x 2} полна в Р 2. Для доказательства возьмем в качестве полной в Р 2 системы U = { x 1& x 2, 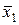 } и выразим х 1& х 2 и
} и выразим х 1& х 2 и 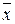 через х 1| x 2 :
через х 1| x 2 :
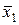 = x 1 | x 1, x 1 & x 2 =
= x 1 | x 1, x 1 & x 2 = 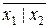 = (x 1| x 2)|(x 1| x 2).
= (x 1| x 2)|(x 1| x 2).
4. Система { x 1 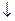 x 2} полна в Р 2. U = { x 1Ú x 2,
x 2} полна в Р 2. U = { x 1Ú x 2, 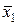 },
}, 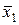 = x 1
= x 1 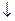 x 1, x 1Ú x 2 = =
x 1, x 1Ú x 2 = = 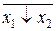 = (x 1
= (x 1 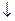 x 2)
x 2) 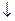 (x 1
(x 1 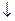 x 2).
x 2).
5. Система { x 1& x 2, x 1Å x 2, 0, 1}, U = { x 1& x 2, 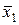 },
}, 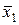 = x 1Å1.
= x 1Å1.
 2015-05-20
2015-05-20 296
296








