Теорема Жегалкина

Каждая функция из 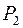может быть представлена в виде полинома Жегалкина единственным образом.

Здесь единственность понимается с точностью до порядка слагаемых в сумме и порядка сомножителей в конъюнкциях:

.

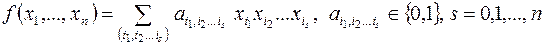Доказательство. Любая функция из 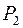может быть представлена формулой над { x ₁& x ₂, x ₁Å x ₂, 0, 1}, а эта формула после раскрытия всех скобок и приведения подобных членов дает полином Жегалкина. Докажем единственность представления. Рассмотрим функции 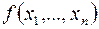от 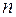переменных. Мы знаем, что всего таких функций, т.е. их таблиц истинности, 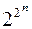. Подсчитаем число различных полиномов Жегалкина от 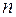переменных. Число наборов 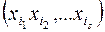равно числу всех подмножеств множества 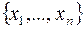, сюда входит и пустое множество (если 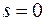). Число подмножеств множества из 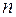элементов равно 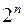, а так как каждый набор входит с коэффициентом 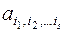, принимающим два значения: 0 или 1, то число всевозможных полиномов будет 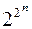. Так как каждому полиному соответствует единственная функция, число функций от 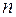переменных равно числу полиномов, то каждой функции будет соответствовать единственный полином.

Определение. Функция 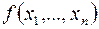, полином Жегалкина для которой имеет следующий линейный относительно переменных вид:

f = а ₀Å а ₁ х ₁Å а ₂ х ₂Å ... Å а_nх_n называется линейной.