Алгебраические дополнения всех элементов матрицы Кирхгофа равны между собой.
Пример 5. Матрица Кирхгофа для графа  на рис. 5
на рис. 5
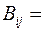
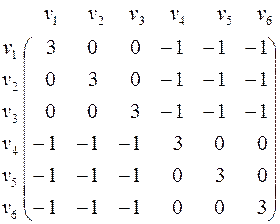
Определение. Простой граф, в котором любые две вершины смежны, называется полным графом и обозначается 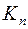 , где
, где 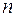 – число вершин.
– число вершин.
Примеры полных графов:
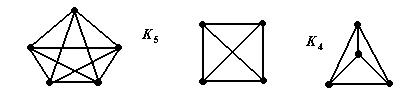 Рис. 8 Рис. 9 Рис. 8 Рис. 9 |
Если степень каждой вершины графа равна 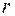 , то граф называется регулярным степени
, то граф называется регулярным степени 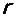 . Графы
. Графы 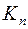 , очевидно, регулярные степени
, очевидно, регулярные степени 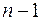 .
.
Допустим, множество вершин графа  можно разбить на 2 непересекающихся подмножества:
можно разбить на 2 непересекающихся подмножества: 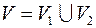 , причем для любого ребра
, причем для любого ребра 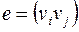 вершины
вершины 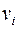 и
и 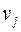 принадлежат разным подмножествам. Такой граф называется двудольным.
принадлежат разным подмножествам. Такой граф называется двудольным.
 Рис. 10 Рис. 11 Рис. 12 Рис. 13 Рис. 10 Рис. 11 Рис. 12 Рис. 13 |
Если каждая вершина из 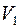 соединена ребром с каждой вершиной из
соединена ребром с каждой вершиной из 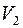 , то такой граф называется полным двудольным графом, обозначается
, то такой граф называется полным двудольным графом, обозначается 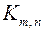 , где
, где 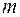 и
и 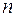 – мощности подмножеств
– мощности подмножеств 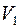 и
и 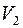 . На рис. 11 и рис. 12 изображены графы
. На рис. 11 и рис. 12 изображены графы 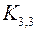 и
и 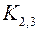 . Среди полных двудольных графов выделяется граф
. Среди полных двудольных графов выделяется граф 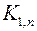 , который называется звездным графом, на рис. 13 изображен граф
, который называется звездным графом, на рис. 13 изображен граф 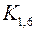 .
.
Для произвольного графа  следующим образом определяется дополнительный граф (или дополнение)
следующим образом определяется дополнительный граф (или дополнение) 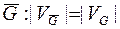 , и любые две несовпадающие вершины смежны в
, и любые две несовпадающие вершины смежны в 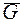 тогда и только тогда, когда они не смежны в
тогда и только тогда, когда они не смежны в  (рис. 14).
(рис. 14).
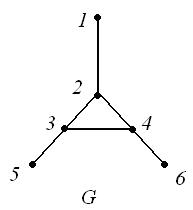 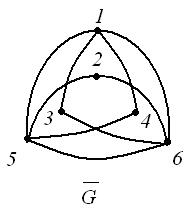 |
| Рис. 14 |
Очевидно, что 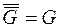 и объединение
и объединение 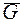 и
и  дает полный граф на том же множестве вершин.
дает полный граф на том же множестве вершин.
Граф изоморфный своему дополнению, называется самодополнительным.
 2015-05-20
2015-05-20 1182
1182








