Теорема о связи вершин с нечетными степенями

Пусть в неориентированном графе есть ровно 2 вершины с нечетными степенями, тогда они связаны.

Доказательство. Пусть 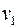и 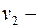вершины с нечетными степенями. Если они принадлежат одной связной компоненте, то они связаны. Если они принадлежат разным связным компонентам, то есть 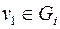, , 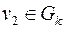то в графе 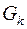, например, всего одна вершина с нечетной степенью, чего не может быть.

Лемма о присоединении ребра. Если 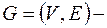связный граф, 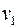и 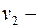две разные его вершины и 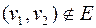, тогда добавление к графу ребра 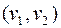приводит к образованию простого цикла.

Доказательство. 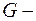связный граф, поэтому существует путь 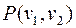, в нем можно выделить подпуть 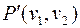, который будет простой цепью.

Путь 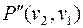, который мы получим, идя из 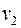в 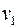по вершинам и ребрам пути 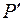, также будет простой цепью. Рассмотрим путь: 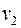, , 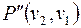, , 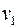, 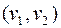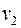он будет простым циклом.

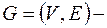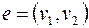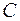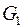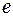Лемма об удалении ребра. Пусть связный граф, ребро входит в цикл , тогда граф , полученный из удалением ребра , будет связным.

Доказательство. Пусть 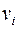и 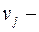произвольные вершины графа. Так как граф связный, то существует путь 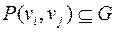. Если этот путь не содержит ребр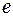о , то 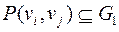, т.е. эти вершины связаны путем и в графе 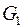. Если 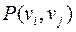проходит по ребру 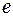, тогда он имеет вид 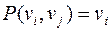, , 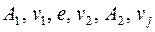где – последовательности ребер и вершин. Ребро 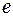входит в цикл 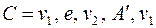, следовательно существует цепь 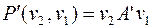тогда существует 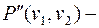противоположная цепь. Рассмотрим в этом случае путь 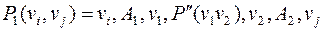, который не содержит ребро 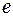и связывает вершины 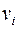и 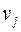в графе 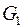, следовательно, 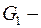связный граф.