2015-05-20
4733
Пусть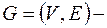 
простой граф (нет петель и кратных ребер), пусть 
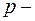число вершин, 
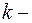число связных компонент, тогда максимальное число ребер в графе будет
.
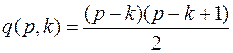Замечание. Для связного графа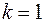 
и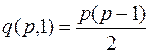 
, а это число ребер в полном графе.
Доказательство. Пусть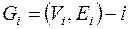 
-тая связная компонента, 
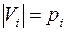, тогда 
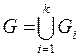. Так как мы хотим получить максимальное число ребер, пусть все связные компоненты – полные графы, число ребер в 
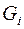ровно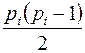 
, а общая сумма ребер будет 
.
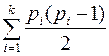Наша цель: не меняя общего числа вершин и числа связных компонент, перестроить граф так, чтобы получить максимальное число ребер.
Рассмотрим две связные компоненты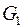 
и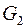 
, и пусть 
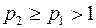. Построим вместо них полные графы 
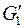и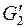 
с числом вершин 
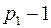и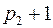 
. Общее число вершин не изменилось, посмотрим, как изменилось число ребер:
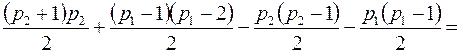
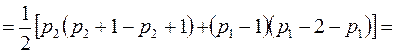
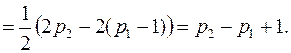
Число ребер увеличилось, как минимум на 1.
Проделаем следующую процедуру:
выберем связную компоненту с наибольшим числом вершин и будем увеличивать число вершин в этой связный компоненте, за счет уменьшения числа вершин в других связных компонентах, при этом общее число ребер будет все время увеличиваться. Очевидно, оно достигает максимума, когда одна компонента будет полным графом с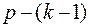 
вершинами, а остальные 
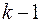компоненты будут изолированными вершинами и число ребер будет
|
|
|
.
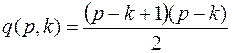Следствие. Если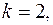 
то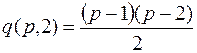 
и это максимальное число ребер при двух связных компонентах. Поэтому, если 
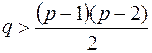, то граф связный.
