Определение. Путем в неориентированном графе 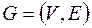 называется любая последовательность вида:
называется любая последовательность вида: 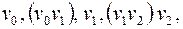
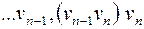 , которая обозначается
, которая обозначается 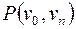 , все
, все 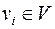 и пары
и пары 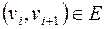 .
.
Путь, где не повторяются ребра, называется цепью. Путь, где не повторяются вершины называется простой цепью. Длиной пути называется число ребер, входящих в путь.
Путь замкнут, если 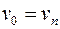 . Замкнутая цепь называется циклом, замкнутая простая цепь – простым циклом.
. Замкнутая цепь называется циклом, замкнутая простая цепь – простым циклом.
Лемма о существовании простой цепи. Пусть 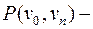 путь из
путь из 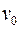 в
в 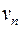 в неориентированном графе
в неориентированном графе  . Тогда можно выбрать подпуть
. Тогда можно выбрать подпуть 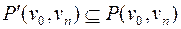 , который будет простой цепью.
, который будет простой цепью.
Доказательство. Если в 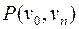 вершины не повторяются, то он и есть простая цепь. Если в этом пути существует повторяющаяся вершина
вершины не повторяются, то он и есть простая цепь. Если в этом пути существует повторяющаяся вершина  , то он имеет вид:
, то он имеет вид:
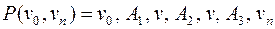 , где
, где 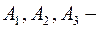 последовательности вершин и ребер.
последовательности вершин и ребер.
Рассмотрим подпуть 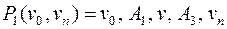 , вершина
, вершина  в этом пути уже не повторяется. Если в
в этом пути уже не повторяется. Если в 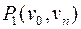 нет повторяющихся вершин, то он и есть простая цепь и теорема доказана. В противном случае повторим процедуру удаления повторяющейся вершины, так как число ребер и вершин конечно, то процесс завершится и мы получим
нет повторяющихся вершин, то он и есть простая цепь и теорема доказана. В противном случае повторим процедуру удаления повторяющейся вершины, так как число ребер и вершин конечно, то процесс завершится и мы получим 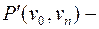 простую цепь.
простую цепь.
Говорят, вершина 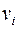 связана с вершиной
связана с вершиной 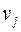 в неориентированном графе, если существует путь
в неориентированном графе, если существует путь 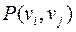 .
.
Определение. Неориентированный граф называется связным, если любые две его вершины связаны.
Связанность вершин задает некоторое отношение 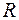 на множестве вершин. Пара
на множестве вершин. Пара 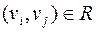 тогда и только тогда, когда существует
тогда и только тогда, когда существует 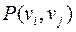 . Будем считать, что
. Будем считать, что 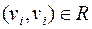 (длина пути в этом случае равна 0). Если
(длина пути в этом случае равна 0). Если 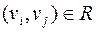 , то
, то 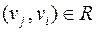 . Если
. Если 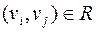 и
и 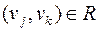 , тогда, очевидно
, тогда, очевидно 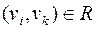 , таким образом, отношение
, таким образом, отношение 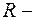 рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
Отношение эквивалентности позволяет разбить множество вершин 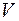 на классы эквивалентности:
на классы эквивалентности:
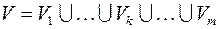 , где
, где 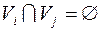 .
.
Две вершины 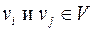 связаны тогда и только тогда, когда они принадлежат одному классу эквивалентности.
связаны тогда и только тогда, когда они принадлежат одному классу эквивалентности.
Определение. Связной компонентой графа 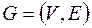 называется подграф
называется подграф 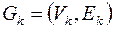 , где
, где 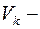 класс эквивалентности на множестве вершин,
класс эквивалентности на множестве вершин, 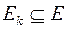 , причем в
, причем в 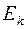 входят все ребра из Е, инцидентные вершинам множества
входят все ребра из Е, инцидентные вершинам множества 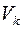 .
.
Каждый неориентированный граф единственным образом представляется в виде объединения своих связных компонент.
На рис. 15 показан граф, состоящий из четырех связных компонент.
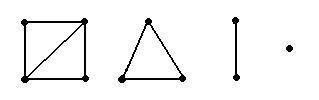 Рис. 15 Рис. 15 |
 2015-05-20
2015-05-20 1544
1544








