2015-05-20
1319
1. метод удлинения
сводится к детализации одного или ряда первичных факторов на факторы более низкого порядка, которые связаны между собой алгебраической зависимостью.
Исходная факторная система: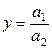 
.
Если а1 представить в виде отдельных слагаемых факторов: а1 = а11+а12+…+а1n, то
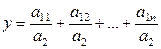- конечная факторная система вида 
.
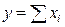Пример: коэффициент закрепления оборотных активов:
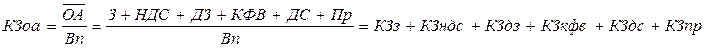где КЗоа – коэффициент закрепления оборотных активов
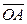– средняя величина оборотных активов
Вп – выручка от продаж
З – средняя величина запасов
НДС – средняя величина налога на добавленную стоимость
ДЗ – средняя величина дебиторской задолженности
КФВ – средняя величина краткосрочных финансовых вложений
ДС – средняя величина денежных средств
Пр – средняя стоимость прочих оборотных активов
2. метод расширения
сводится к введению в модель нового фактора, т.е. к умножению и одновременно делению на этот новый фактор одного или ряда факторов первого порядка и соединению их в новом сочетании.
Исходная факторная система: .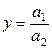
Если и числитель, и знаменатель дроби «расширить» умножением на одно и то же число, то получим новую факторную систему:
,
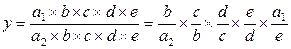то есть мультипликативную модель вида: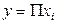 
.
Пример:
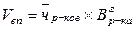
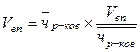
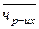
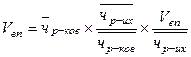
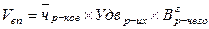ФЧД
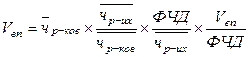
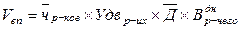ФЧЧ
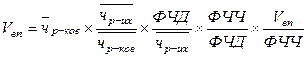
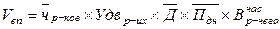
3. метод сокращения
применяется только для преобразования кратных моделей.
сводится к тому, что числитель и знаменатель делятся на один и тот же фактор, при этом форма связи между факторами не меняется.
Исходная факторная система: .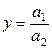
Если числитель и знаменатель дроби разделить на одно и то же число при соблюдении правил выделения факторов, то получим новую факторную систему: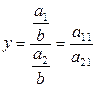 
. В данном случае имеет конечную факторную систему вида: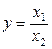 
Пример: рентабельность совокупного капитала
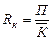Вп
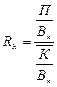
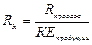
где П – прибыль
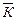- средняя величина капитала предприятия
Вп – выручка от продаж
Rпродаж – рентабельность продаж
КЕпродукции – капиталоемкость продукции
