Метод Гаусса. Метод Гаусса является прямым методом решения систем линейных уравнений

Метод Гаусса является прямым методом решения систем линейных уравнений. Он наиболее универсален. Ограничений, кроме равенства нулю определителя матрицы А, практическине имеет. При определителе, близком к нулю, мы можем получить плохо обусловленную систему (см. главу 1).

Алгоритм метода состоит из двух этапов [5]. Первый называется прямым ходом. Он заключается в последовательном исключении неизвестных из уравнений, начиная с х₁.

Из первого уравнения системы (3.1) выражаем неизвестное х₁.

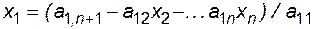, (3.6),

где ,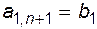

что возможно при 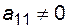, в противном случае надо осуществить перестановку уравнений системы. Согласно формуле (3.6), необходимо каждый элемент первой строки расширенной матрицы поделить на диагональный элемент:

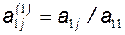. (3.7)

Затем подставляем выражение (3.6) во все остальные уравнения системы, тем самым исключаем х₁ из всех уравнений, кроме первого. Элементы расширенной матрицы преобразуем по формуле:

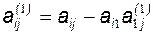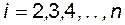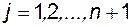, , . (3.8)

B результате исключения первого неизвестного х₁ из всех уравнений все элементы первого столбца преобразованной матрицы будут равны нулю, кроме а₁₁⁽¹⁾= 1.

Неизвестное х₂ выразим из второго уравнения системы и исключим из остальных уравнений и т.д. В результате получим систему с верхней треугольной матрицей, у которой все элементы ниже главной диагонали равны нулю.

Запишем выражения для неизвестных х_k и преобразования элементов расширенной матрицы системы, которые обобщают

формулы (3.6) - (3.8):

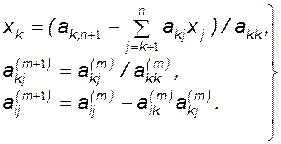(3.9)

Второй этап решения называется обратным ходом метода Гаусса и состоит в последовательном определении неизвестных х_k по первой формуле (3.9), начиная с неизвестного x_n и заканчивая x₁.

Точность результатов определяется точностью выполнения арифметических операций при преобразовании матрицы А. Для уменьшения погрешности при делении на диагональный элемент (вторая формула (3.9)) осуществляют перестановку уравнений с целью постановки на диагональ наибольшего по модулю из всех элементов данного столбца. Это называется выбором главного элемента столбца.

Количество арифметических операций в методе Гаусса зависит от размерности системы и примерно равно 2/3n³ [1]. Контроль полученных решений можно провести путем их подстановки в исходную систему и вычисления невязок между правыми и левыми частями уравнения:

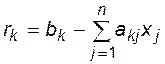. (3.10)