Задачи электротехники, приводящие к решению систем линейных уравнений

Лекция 3

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Задачи электротехники, приводящие к решению систем линейных уравнений

Расчет токов и напряжений в электрических цепях часто сводится к решению системы из n (число неизвестных величин) линейных алгебраических уравнений

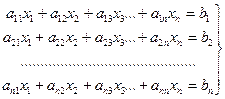(3.1)

или в матричной форме записи:

A X = B, (3.2)

где

A = 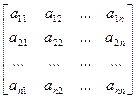- матрица коэффициентов;

B= 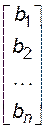-столбец правых частей; X= 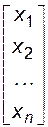- столбец неизвестных.

Используется также и расширенная матрица системы A_р, полученная добавлением столбца n+1 к матрице А. Элементы этого столбца равны соответствующим элементам столбца свободных

членов В - а_i,n+1=b_i:

A_р = 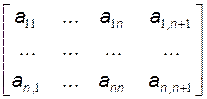(3.3)

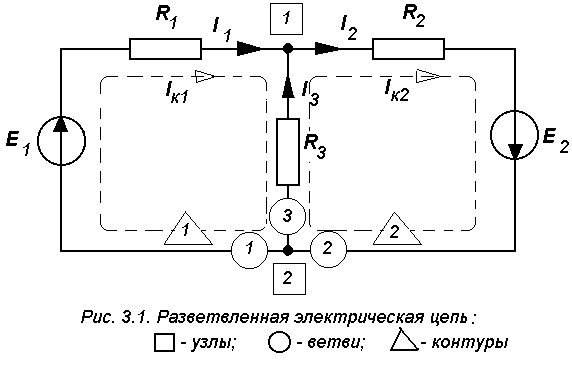На рис.3.1 изображена разветвленная электрическая схема постоянного тока.

Как правило, в таких схемах при заданных активных сопротивлениях R и электродвижущих силах (ЭДС) Е требуется найти токи I. Одним из способов расчета таких схем является составление уравнений для токов ветвей на основании законов Кирхгофа с последующим их решением [4]. Составим эти уравнения.

По первому закону Кирхгофа - алгебраическая сумма токов подтекающих к узлу, равна нулю (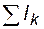 = 0, где k - номер узла), имеем для узла 1:

.

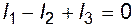По второму закону Кирхгофа - алгебраическая сумма падений напряжений по любому замкнутому контуру равна алгебраической сумме ЭДС по этому контуру (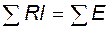 ) - выбирая контуры и положительные направления в них как на рис.3.1, получим:

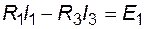- для контура 1,

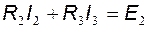- для контура 2.

Получили 3 уравнения для трех неизвестных токов. Приведем данные уравнения к виду (3.1), вводя нулевые коэффициенты при отсутствующих в уравнениях токах по второму закону Кирхгофа и 1 или -1 в уравнении, составленном по первому закону Кирхгофа:

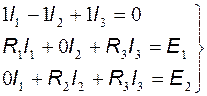(3.4)

или в матричной форме записи

RI=E. (3.5)

Сравнивая (3.4) c (3.1) видим, что матрица R есть матрица А, столбец Е - столбец В, столбец I - столбец неизвестных X.

R = 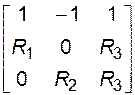- матрица сопротивлений;

Е = 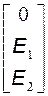- столбец ЭДС контуров; I = 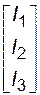- столбец токов.

Решив полученную систему относительно неизвестных токов I₁,I₂ и I₃,получим требуемый результат. Если один или несколько токов получатся со знаком минус, то это будет означать, что реальное направление тока противоположно принятому направлению при составлении исходных уравнений.

К решению систем линейных алгебраических уравнений приходится прибегать также при численном интегрировании систем обыкновенных дифференциальных уравнений (см. главу 4), с помощью которых решаются задачи динамики (переходные процессы) электрических и электромеханических систем. Для них и для других задач приходится находить определители матриц,обратные матрицы,собственные числа матриц и т. д.[1,5,6,10]. Все это находится с помощью решения систем линейных алгебраических уравнений.

Существуют два класса методов решения систем уравнений: прямые и итерационные. Прямые методы являются универсальными и применяются для решения систем сравнительно невысокого порядка (n < 200 - 250) [1]. Итерационные методы выгодно использовать для систем высокого порядка со слабо заполненными матрицами, то есть с матрицами, у которых относительно мало число ненулевых элементов a_ij. Такие матрицы могут быть, например, при расчетах сложных электрических цепей, имеющих много узлов, примером которых могут служить системы электроснабжения района, области и т.д. Также в электротехнике стараются с помощью различных приемов сократить число неизвестных, входящих в систему. Например, для схемы на рис.3.1 можно уменьшить число уравнений в системе до двух, если за неизвестные принять токи, якобы протекающие в первом и втором контурах - контурные токи I_1к и I_2к, а реальные токи ветвей вычислить потом отдельно: I₁ = I_1к, I₂=I_2к , I₃ = - I_1к+ I_2к [4].

Рассмотрим три метода решения систем линейных алгебраических уравнений - Гаусса, простых итераций и Зейделя, дающих представление о прямых и итерационных методах и наиболее часто применяемых в расчетной практике.