Степенной базис

Выберем базисные функции 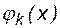в виде последовательности степеней аргумента х, которые линейно независимы.

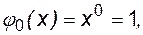
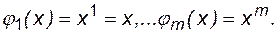(6.22)

Степенной базис интересен тем, что при количестве базисных функций 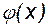, равном количеству узлов аппроксимируемой функции (m=n), мы получаем полиномиальную интерполяцию. Это может служить проверкой правильности программ, реализующих алгоритмы МНК.

На практике степень полинома m выбирают значительно меньше n. Аппроксимирующая кривая в МНК не проходит через узлы функции и «сглаживает» экспериментальную кривую (кроме m=n).

Запишем матрицу Грама и столбец правых частей для степенного базиса:

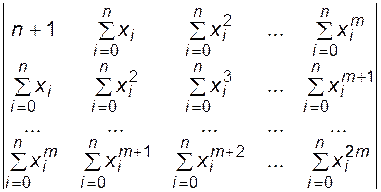и 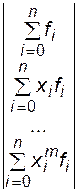. (6.23)

Из формул (6.23) следует, что в матрице Грама нужно вычислить лишь элементы первого и последнего столбца. Остальные элементы заполняются путем циклического присвоения.

Процедура-подпрограмма Gram формирования матрицы Грама и столбца свободных членов приведена в конце главы (ПРОГРАММА 6.3).

В силу причин, сказанных выше, в процедуре использован тип действительных переменных EXTENDED. Элементы матрицы Грама формируются процедурой функцией El_Gram, которая использует процедуру функцию возведения действительного числа в целую степень Step_X.

Для иллюстрации работы программы аппроксимации в реализующей модель электромагнита замка программе был использован генератор случайных чисел, с помощью которого вносилась случайная погрешность в таблицу результатов расчета тока аналитическим методом. Данные результаты записывались в файл наряду с точными значениями тока. Это позволило наглядно представить результаты аппроксимации.

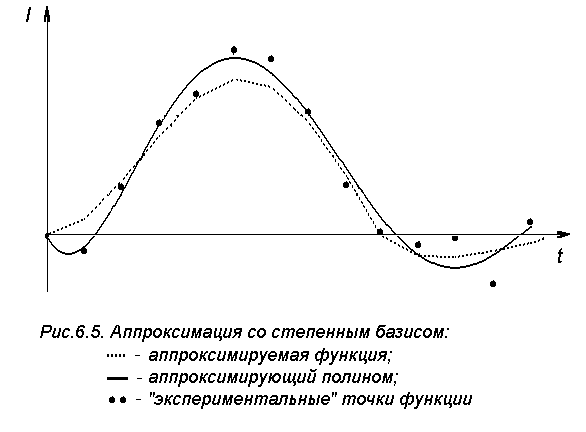
На экран выводятся сразу и реальная кривая и точки «измерений с погрешностью», и аппроксимирующая кривая. На рис.6.5 изображены результаты аппроксимации кривой тока полиномом пятой степени при 14 "экспериментальных" точках.

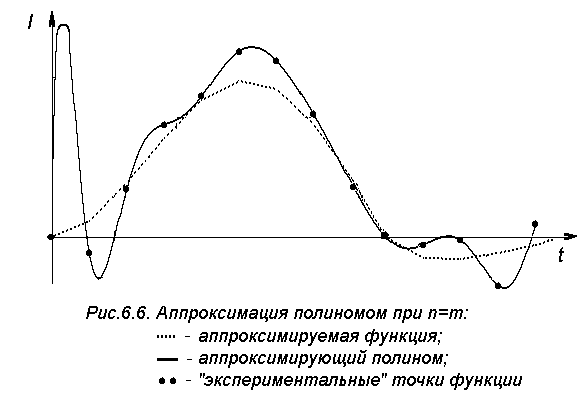
Проверкой правильности программы аппроксимации служит условие, что при m=n аппроксимирующий полином должен проходить через все узлы аппроксимируемой функции, при этом среднеквадратичное отклонение равно нулю. Результат расчета при m=n приведен на рис.6.6.

Линейный вариант метода наименьших квадратов

В электротехнической практике часто приходится измерять активные сопротивления обмоток электрических машин и других устройств. Достаточно часто это делается с помощью амперметра и вольтметра (метод амперметра-вольтметра). Изменяют постоянное напряжение U на обмотке и записывают значения тока I, проходящего по ней. Получается таблица значений U и I. Здесь аргументом x является напряжение, а функцией f(x) - ток. Если пренебречь очень малым изменением сопротивления от температуры, то зависимость между током и напряжением представляет прямую линию – I=U/R (y=ax, а=1/R, R - активное сопротивление обмотки ).

Такие аналитические зависимости имеют место во всех электрических цепях с постоянными параметрами, а сами цепи называются линейными. В этом и подобном случаях при аппроксимации экспериментальных данных достаточно ограничиться полиномом первой степени, то есть прямой линией.

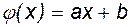или 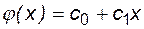(6.24)

где 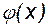- линейная аппроксимирующая функция.

Для коэффициентов а и b из общего алгоритма МНК получаются следующие выражения:

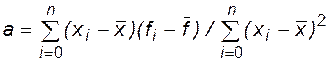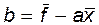, , (6.25)

где 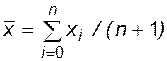, 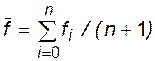; n+1 - количество узлов; x_i,f_i - узлы и значения аппроксимируемой функции в них.

Программа аппроксимации со степенным базисом при задании ей степени аппроксимирующего полинома равной единице находит значения a и b (с₁ и с₀ соответственно). Поэтому ее можно использовать и в линейном варианте МНК. Но если реализовать линейный вариант МНК в виде отдельной программы, то она будет много проще, чем программа для степенного базиса.

Составление и отладка программы линейного варианта МНК по формулам (6.24-6.25) проводится студентами самостоятельно на практических занятиях. Результаты работы программы тестируются с помощью программы, реализующий степенной базис.

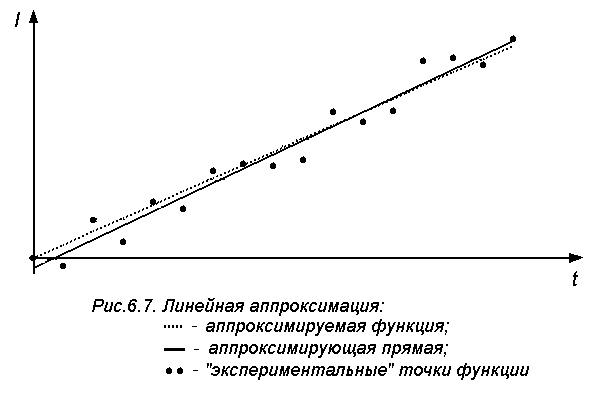
На рис 6.7 представлена аппроксимация тока катушки при его линейном росте, что получается при определенном соотношении между параметрами цепи и приложенной ЭДС. «Экспериментальные» точки получены способом, описанным выше. Как видно из рисунка, аппроксимирующая прямая достаточно близка к исходной зависимости даже при существенном разбросе "опытных" данных.

В пособии не рассматриваются вопросы численного дифференцирования, к которому приходится прибегать при невозможности найти производные функции аналитически. Зная, что дифференцирование есть действие, обратное интегрированию, можно при нахождении производных воспользоваться результатами аппроксимации функциональных зависимостей. Из рассмотренных нами методов аппроксимации кусочно-линейный дает первую производную как набор констант на интервалах интерполяции со скачками в узлах. Остальные производные будут равны нулю. Полиномиальная аппроксимация дает непрерывные производные, определяемые степенью полинома. Из этого следует, что аппроксимация кубическими сплайнами позволяет вычислить первую, вторую и третью производные.

ПРОГРАММА 6.1

{__Необходимые описания в вызывающей программе _______}

Const Nm=55; { Максимально возможное число точек

в интерполируемой функции }

Type

{ Массивные типы для формирования матриц коэффициентов }

Mat = Array [0..Nm,0..Nm] Of Extended;

VecF = Array [0..Nm] Of Extended;

Vec = Array [0..Nm] Of Real;

{-- Процедура-подпрограмма формирования матриц для нахождения коэффициентов интерполяционного полинома }

Procedure Canon(N:Integer; Var Ac:Mat; Var F:VecF; Fun:Vec; X:Vec);

{ N - количество точек }

{ Ac - матрица коэффициентов при параметрах Сi }

{ Fun - столбец значений функции }

{ X - столбец значений аргумента }

{ F - столбец значений функции повышенной точности }

Var

i,j,k:Integer; {Параметры циклов }

R,S:Extended; { Вспомогательные переменные }

Begin

For i:=0 to N do Begin R:=1.0; S:=X[i]; F[i]:=Fun[i];

For j:=0 to N do Begin Ac[i,j]:=R; R:=R*S End End;

End; {Canon___________________________________________}

ПРОГРАММА 6.2

{ Описание типов и переменных, необходимых для формирования коэффициентов сплайнов }

Const Nmax=70; { Максимальное число точек интерполируемой

функции }

Type

{Типы для применяемых в программе массивов }

Vec = array [0..NMax] Of Real;

Matr = array [1..NMax,1..NMax] Of Real;

Var

a,b,c,d { Коэффициенты сплайнов }

h, { Шаги аргумента интерполируемой функции }

p, { Правая часть системы для расчета коэффициента с }

cv { Вспомогательный массив при определении с }

F,x, { Значения функций и аргумента в точка }

:Vec;

Кc { Матрица коэффициентов при нахождении с }:Matr;

N { Текущая размерность задачи }:Integer;

Ms { Сообщение процедур Gauss при аварийном ее заверше-

нии }

{________________________________________________________}

--------------

{_____________Формирование матрицы Kc ___________________

______________для расчета коэффициентов с_i _______________}

c[1]:=0; c[N+1]:=0; { Значения коэффициента на концах интервала }

{ Расчет массива шагов аргумента }

For i:=1 to N do h[i]:=(x[i]-x[i-1]);

{ Расчет столбца правых частей системы для поиска с }

j:=0;

For i:=2 to N do Begin

i:=i+1;

p[j]:=3.0*((F[i]-F[i-1])/h[i]-(F[i-1]-F[i-2])/h[i-1]);

End;

{ Формирование матрицы для расчета коэффициентов сv }

Kc[1,1]:=2.0*(h[1]+h[2]);

Kc[1,2]:=h[2];

Kc[N-1,N-2]:=h[N-1];

Kc[N-1,N-1]:=h[N-1]+2.0*(h[N-1]+h[N]);

j:=-1;

For i:=2 to N-2 do Begin i:=i+1;

Kc[i,1+j]:=h[i-1]; Kc[i,2+j]:=2.0*(h[i-1]+h[i]); Kc[i,3+j]:=h[i];

End;

{ Расчет коэффициентов сv методом Гаусса }

Gauss(N-1,Kc,p,cv,Ms);

{____Присвоение значений массиву коэффициентов с_________ }

For i:=2 to N do c[i]:=cv[i-1];

{_____Расчет остальных коэффициентов сплайнов ___________}

For i:=1 to N do Begin

a[i]:=F[i-1];

b[i]:=(F[i]-f[i-1])/h[i] - (c[i+1]+2.0*c[i])*h[i]/3.0;

d[i]:=(c[i+1]-c[i])/(3.0*h[i]); End;

{ ______________ Продолжение программы.______________......}

ПРОГРАММА 6.3

{ Необходимые описания в вызывающей программе }

Const Nm=55; { Максимально возможная размерность задачи }

Type

{Массивные типы для процедуры Gram }

Mat = Array [0..Nm,0..Nm] Of Extended;

Vec = Array [0..Nm] Of Extended;

{________________________________________________________}

---------

{_Процедура формирования матрицы Грама ______________}

{___и столбца свободных членов при степенном базисе ____}

Procedure Gram(N,M:Integer; x,F:vec; var M_G:mat; Var B:vec);

{ N - количество узлов аппроксимируемой фунцнкции }

{ M - степень аппроксимирующего полинома }

{ F,x - массивы аргумента и функции }

{ M_G - сформированная матрица Грама }

{ B - сформированный вектор правых частей }

Var i,j:Integer; { Для организации циклов }

{Процедура-функция формирования элемента матрицы Грама }

Function El_Gram(N,M:Integer; Flag:Integer):Extended;

Var i,j:Integer; { Для организации циклов }

Sum:Extended; { Вспомогательное переменное }

{ Возведение числа в целую степень }

Function Step_X(M:Integer; x:Extended): Extended;

Var i:Integer; { Для организации циклов }

Proizv:Extended; { Вспомогательное переменное }

Begin

If M > 0 Then Begin Proizv:=1.0;

For i:=1 to M do Proizv:=Proizv*X;

Step_X:=Proizv End

Else Step_X:=1.0; { Нулевая степень числа }

End; {Step_X _____________________________________________}

Begin

Sum:=0.0;

If Flag = 1 Then For i:=1 to N do Sum:=Sum+Step_X(M,x[i])

Else For i:=0 to N do Sum:=Sum+Step_X(M,x[i])*F[i];

If (Flag = 1) And (M = 0) Then El_Gram:=N+1

Else El_Gram:=Sum;

End; { El_Gram __________________________________________}

{___ Исполняемая часть процедуры Gram____________________}

Begin

{ Первый столбец матрицы Грама }

j:=0;

For i:=0 to M do M_G[i,j]:=El_Gram(N,i+j,1);

{ Последний столбец матрицы Грама}

j:=M;

For i:=1 to M do M_G[i,j]:=El_Gram(N,i+j,1);

{Циклическое присвоение значения другим элементам }

For i:=1 to M do

For j:=0 to M-i do M_G[j,i]:=M_G[j+i,0];

For i:=1 to M-1 do

For j:=M-i+1 to M do M_G[j,i]:=M_G[i+j-M,M];

{ Столбец правых частей }

For i:=0 to M do

B[i]:=El_Gram(N,i,2);

End; Gram________________________________________________}