Интерполяция кубическими сплайнами

Недостатки кусочно-линейной и полиномиальной интерполяции привели к разработке теории сплайн-функции (от английского слова spline - линейка, рейка). Это связано с тем, что в инженерной практике часто приходится проводить гладкие кривые, используя упругую металлическую линейку, закрепленную в узловых точках.

Рассмотрим наиболее распространенный вариант сплайн-интерполяции - интерполяцию кубическими сплайнами [5].

Установлено, что упругая недеформируемая линейка проходит между соседними узлами по линии, удовлетворяющей уравнению

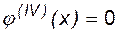. (6.8)

Очевидно, если в качестве функции 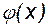выбрать полином, то его степень должна быть не выше третьей, так как для полинома третьей степени четвертая производная тождественно равна нулю. Этот полином называют кубическим сплайном, который на интервале [x_i-1,x_i] записывается в виде

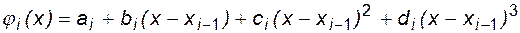, (6.9)

где a_i,b_i,c_i,d_i - коэффициенты сплайна, определяемые из дополнительных условий; i = 1,2,3,....n - номер сплайна.

Всего сплайнов на один меньше, чем точек интерполяции. Интерполяцию сплайнами можно назвать кусочно-полиномиальной.

Коэффициенты сплайнов определяются из следующих условий сшивания соседних сплайнов в узловых точках.

1. Равенство значений сплайнов 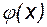и функции f(x) в узловых точках - условия Лагранжа:

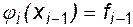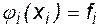, . (6.10)

2. Непрерывность первой и второй производных от сплайнов в узлах:

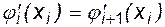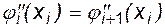, . (6.11)

Кроме перечисленных условий, следует добавить условия на концах, т. е. в точках x₀ и x_n. В общем случае эти условия зависят от конкретной задачи. Мы воспользуемся условиями свободных концов сплайнов, т.е. вне интервала [x₀,x_n] функция описывается полиномом первой степени - прямой линией:

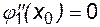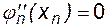, . (6.12)

Условия (6.10)-(6.12) позволяют найти коэффициенты a_i,b_i,c_i,d_i всех n сплайнов. Их значения выражаются следующими формулами:

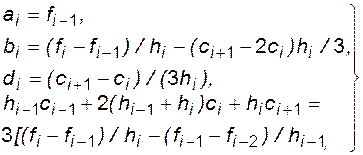, (6.13)

где в первых трех уравнениях i = 1,2,...n, а в третьем i = 2,3,..n;

h_i=x_i-x_i-1 - i -й шаг аргумента.

Учитывая индексацию для с_i, добавим значения этого коэффициента на концах сплайна

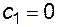и 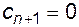. (6.14)

Сначала решается система из n - 1 линейных уравнений для с_i. Затем определяются b_i и d_i по известным коэффициентам с_i, а_i известно - это значения функции f(x) в узловых точках. В каждое уравнение для определения с_i входит только три неизвестных с последовательными значениями индексов c_i-₁,c_i,c_i+1. Такая матрица, имеющая отличные от нуля только элементы главной и двух соседних диагоналей, называется трехдиагональной.

Программная реализация рассмотренного алгоритма приведена ниже (ПРОГРАММА 6.2). Приведен фрагмент, в котором рассчитываются коэффициенты сплайнов по узловым значениям интерполируемой функции.

Для формирования трехдиагональной матрицы Kc использован массив шагов аргумента h_i. В процедуре Gauss рассчитывается вспомогательный массив cv, имеющий на 2 элемента меньше, чем массив с., так как с₀ и c_n+1 известны и равны нулю. При большом числе уравнений для решения систем с трехдиагональной матрицей применяют метод прогонки [6], являющийся вариантом метода последовательных исключений. Результаты расчетов с использованием интерполяции сплайнами приведены на рис.6.4. В качестве интерполируемой функции был взят ток катушки электромагнита.

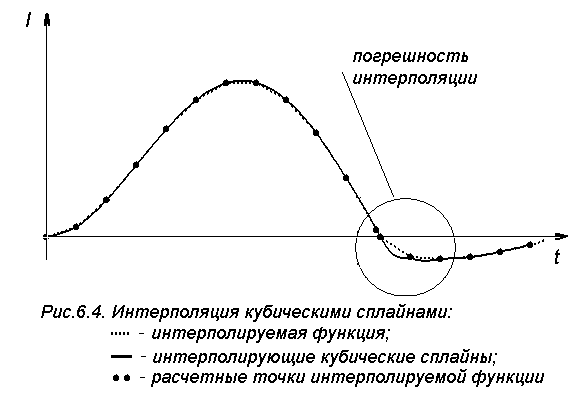
Как видно на рис.6.4, интерполяция кубическими сплайнами дает очень хорошее приближение в случае, если функция гладкая. В окружности на рисунке обозначен участок, где погрешность сплайна велика. Это связано с тем, что на этом участке происходит излом кривой тока, связанный с изменением сопротивления диода R_D c прямого R_пр на обратное R_обр. При этом первая производная тока делает скачок, а сплайны по определению имеют равные первые производные справа и слева от узловой точки.

Как отмечалось ранее, интерполяция есть частный случай аппроксимации, критерием которой являются условия Лагранжа. Рассмотрим другой критерий аппроксимации - минимизацию среднеквадратичного отклонения приближающей функции 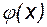от аппроксимируемой f(x).