Напомним определение перпендикулярных векторов на плоскости и в трехмерном пространстве.
Определение.
Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам (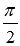 радиан).
радиан).
Теорема.
Для перпендикулярности двух ненулевых векторов 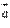 и
и 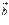 необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство
необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство  .
.
Доказательство.
Пусть векторы 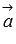 и
и 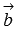 перпендикулярны. Докажем выполнение равенства
перпендикулярны. Докажем выполнение равенства 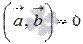 .
.
По определению скалярное произведение векторов равно произведению их длин на косинус угла между ними. Так как векторы 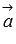 и
и 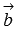 перпендикулярны, то угол между ними равен девяноста градусам, следовательно,
перпендикулярны, то угол между ними равен девяноста градусам, следовательно,  , что и требовалось доказать.
, что и требовалось доказать.
Переходим ко второй части доказательства.
Теперь считаем, что  . Докажем, что векторы
. Докажем, что векторы 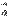 и
и 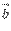 перпендикулярны.
перпендикулярны.
Так как векторы 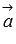 и
и 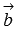 ненулевые, то из равенства
ненулевые, то из равенства 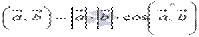 следует, что
следует, что  . Таким образом, косинус угла между векторами
. Таким образом, косинус угла между векторами 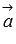 и
и 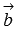 равен нулю, следовательно, угол
равен нулю, следовательно, угол  равен
равен 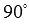 , что указывает на перпендикулярность векторов
, что указывает на перпендикулярность векторов 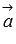 и
и 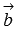 .
.
|
|
|
Итак, необходимое и достаточное условие перпендикулярности двух векторов полностью доказано.
Как же выглядит условие перпендикулярности двух векторов в координатной форме?
В разделе скалярное произведение в координатах мы показали, что для двух векторов с заданными координатами  и
и  на плоскости справедливо равенство
на плоскости справедливо равенство  , а для двух векторов
, а для двух векторов  и
и  в пространстве
в пространстве  . Таким образом, необходимое и достаточное условие перпендикулярности двух векторов в координатах имеет вид
. Таким образом, необходимое и достаточное условие перпендикулярности двух векторов в координатах имеет вид 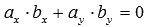 на плоскости, а в трехмерном пространстве
на плоскости, а в трехмерном пространстве 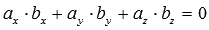 .
.
Рассмотрим применение полученных условий на практике, для этого разберем решение нескольких примеров.
Пример.
Перпендикулярны ли векторы 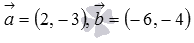 .
.
Решение.
Вычислим их скалярное произведение по координатам  . Следовательно, условие перпендикулярности двух векторов на плоскости выполнено, то есть, они перпендикулярны.
. Следовательно, условие перпендикулярности двух векторов на плоскости выполнено, то есть, они перпендикулярны.
Ответ:
да, векторы перпендикулярны.
Пример.
Перпендикулярны ли векторы 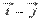 и
и  , где
, где  - координатные векторы прямоугольной системы координат в трехмерном пространстве.
- координатные векторы прямоугольной системы координат в трехмерном пространстве.
Решение.
Векторы 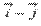 и
и  имеют соответственно координаты
имеют соответственно координаты 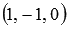 и
и 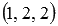 (при необходимости смотрите статью координаты вектора в прямоугольной системе координат). Проверим выполнение необходимого и достаточного условия перпендикулярности двух векторов:
(при необходимости смотрите статью координаты вектора в прямоугольной системе координат). Проверим выполнение необходимого и достаточного условия перпендикулярности двух векторов:
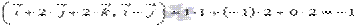
Так как  , то векторы
, то векторы 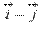 и
и  не перпендикулярны.
не перпендикулярны.
Ответ:
нет, не перпендикулярны.
Пример.
Найдите значение 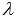 , при котором векторы
, при котором векторы 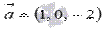 и
и  перпендикулярны.
перпендикулярны.
Решение.
Воспользуемся условием перпендикулярности двух векторов в пространстве в координатной форме
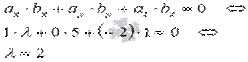
Ответ:
векторы перпендикулярны при 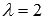 .
.
В некоторых случаях возможно ответить на вопрос о перпендикулярности двух векторов без использования необходимого и достаточного условия перпендикулярности. Например, когда известны длины всех сторон треугольника, построенного на двух векторах, то можно найти угол между векторами и посмотреть, равен ли он девяноста градусам.
|
|
|
Пример.
Стороны АВ, АС и ВС треугольника АВС равны соответственно 8, 6 и 10 см. Убедитесь, что векторы 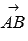 и
и 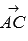 перпендикулярны.
перпендикулярны.
Решение.
Если векторы 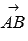 и
и 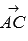 перпендикулярны, то треугольник АВС – прямоугольный и его гипотенузой является сторона ВС. Тогда по теореме Пифагора должно выполняться равенство
перпендикулярны, то треугольник АВС – прямоугольный и его гипотенузой является сторона ВС. Тогда по теореме Пифагора должно выполняться равенство 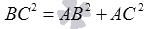 . Проверим его справедливость:
. Проверим его справедливость: 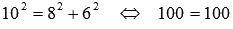 .
.
Следовательно, АВ и АС – катеты прямоугольного треугольника АВС, поэтому, векторы 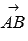 и
и 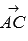 перпендикулярны.
перпендикулярны.
 2015-05-20
2015-05-20 5682
5682








