Начнем с постановки задачи.
Пусть нам требуется найти координаты вектора в трехмерном пространстве, который одновременно перпендикулярен двум не коллинеарным векторам 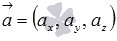 и
и 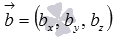 . Если векторы
. Если векторы 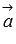 и
и 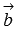 коллинеарные, то решением задачи будет вектор, перпендикулярный одному из векторов
коллинеарные, то решением задачи будет вектор, перпендикулярный одному из векторов 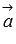 или
или 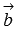 (о нахождении такого вектора мы говорили в предыдущем пункте).
(о нахождении такого вектора мы говорили в предыдущем пункте).
Одно из решений такой задачи основано на использовании понятия векторного произведения векторов.
Нам известно, что векторное произведение векторов 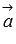 и
и 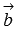 представляет собой вектор, перпендикулярный одновременно и вектору
представляет собой вектор, перпендикулярный одновременно и вектору 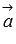 и
и 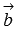 . Таким образом, векторное произведение
. Таким образом, векторное произведение  является решением нашей задачи. В координатной форме оно имеет вид
является решением нашей задачи. В координатной форме оно имеет вид
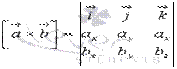
Разберем на примере.
Пример.
Найдите координаты какого-нибудь вектора, перпендикулярного одновременно двум векторам 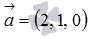 и
и 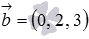 .
.
Решение.
Решением нашей задачи является векторное произведение заданных векторов. Найдем его (при необходимости смотрите статью вычисление определителя матрицы):
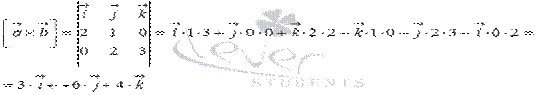
Ответ:
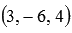 - один из векторов, одновременно перпендикулярный и вектору
- один из векторов, одновременно перпендикулярный и вектору 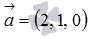 и
и 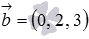 .
.
|
|
|
 2015-05-20
2015-05-20 21299
21299








