3.1.1. Задача отыскания параметров эмпирической формулы является одной из наиболее важных задач, встречающихся при обработке результатов наблюдений, различных экспериментов и т.п. Ее суть в следующем.
Имеется m точек, заданных координатами в декартовой системе координат (xi,yi), i=1,…,m. Требуется найти такую функцию y=f(x), значения которой в точках xi как можно более точно совпадают с yi., т. е. yi»f(xi), см. рис.
Слова «наилучшее приближение к имеющимся данным» могут пониматься по-разному. Наиболее часто используется так называемый принцип наименьших квадратов. Он основан на том, что из заданного множества формул вида y=f(x) наилучшей является та функция, для которой сумма квадратов отклонений вычисленных значений f(xi) от наблюдаемых значений yi является наименьшей. Подбор параметров функции f(x), основанный на этом принципе, называют методом наименьших квадратов.
Рассмотрим метод наименьших квадратов на примере эмпирической формулы, которая линейно зависит от 2-х параметров и имеет вид:
f(x)=f(x, a, b)=aj(x)+by(x). (1)
Заметим, что линейная зависимость формулы от параметров взята не случайно. В этом случае метод наименьших квадратов имеет наиболее простую и изящную реализацию. Что касается двух параметров, то это не принципиально, с двумя параметрами проще.
Введем в рассмотрение функцию, представляющую сумму квадратов отклонений:
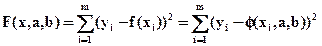 . (2)
. (2)
В соответствии с принятым подходом, параметры a и b необходимо подобрать таким образом, чтобы значение F(x,a,b) было минимальным:
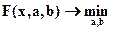 . (3)
. (3)
Как известно из курса высшей математики, точка минимума (a,b) необходимо удовлетворяет условиям:
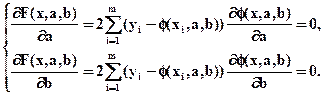 (4)
(4)
Подставляя в систему (4) функцию (1), получаем:
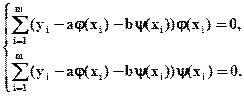 (5)
(5)
После несложных преобразований приходим к системе уравнений
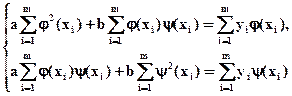 (5)
(5)
Решив систему (5), найдем значения параметров a и b, которые являются решением задачи (2).
Система (5) представлена в общем виде. Ее конкретный вид зависит от функций j(x), y(x). Рассмотрим примеры.
Пример 1. Пусть f(x,a,b)=ax+b, т.е. j(x)=x, y(x)=1. Система (5) принимает вид
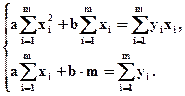
Пример 2. Пусть f(x,a,b)=a×sinx+b×lnx, т.е. j(x)=sinx, y(x)=lnx. Система (5) принимает вид
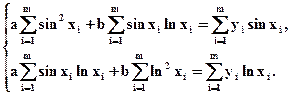
3.1.2. Проведенные выше рассуждения нетрудно обобщить на случай 3-х, 4-х и более параметров, от которых искомая функция зависит линейно. Например, если
f(x)=f(x, a, b, c)=aj(x)+by(x)+cl(x),
то система для отыскания параметров a, b, c принимает вид
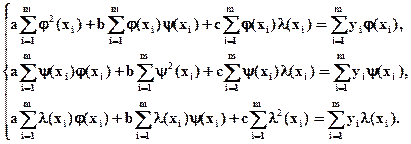
3.1.3. Для подбора подходящей эмпирической формулы необходимо знать, как выглядят графически математические зависимости, из которых выбирается эмпирическая формула. Приведем графики тех из них, которые будут использоваться в настоящей лабораторной работе.
a) y=ax+b (линейная зависимость)
a>0 a<0
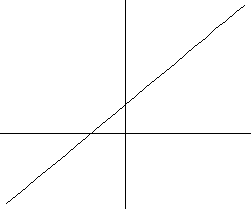
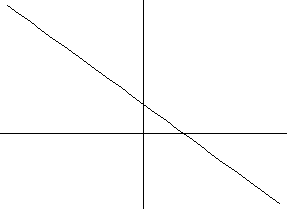
2) y=ax2+bx+c (квадратичная зависимость)
a>0 a<0
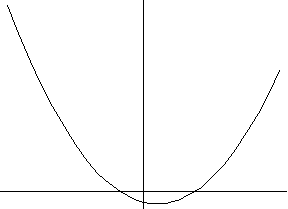
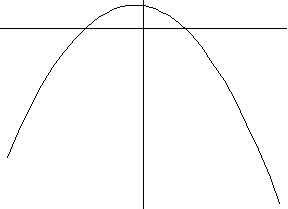
3) y=a/x+b (гиперболическая зависимость)
a>0 a<0
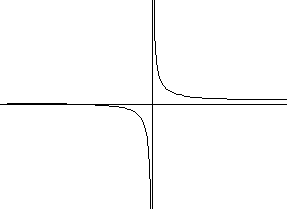
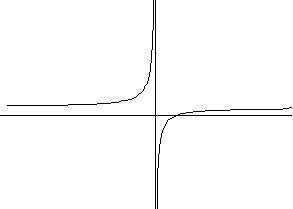
3) y=aex+b (показательная зависимость)
a>0 a<0
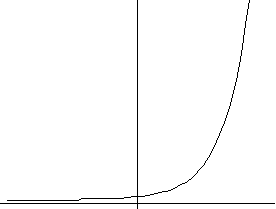
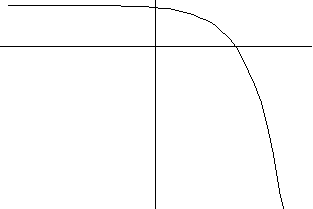
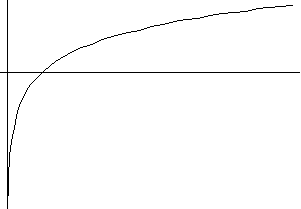
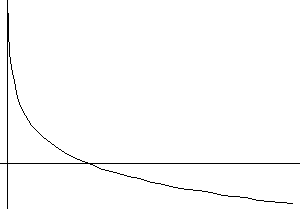
5) y=a lnx+b (логарифмическаяая зависимость)
a>0 a<0
6) 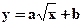
a>0 a<0
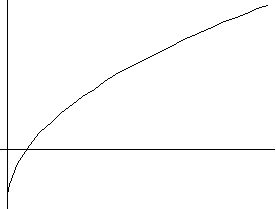
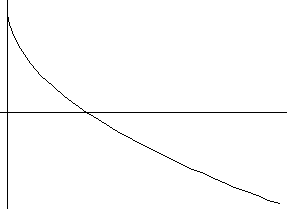
7) y=a sinx + b cosx + c
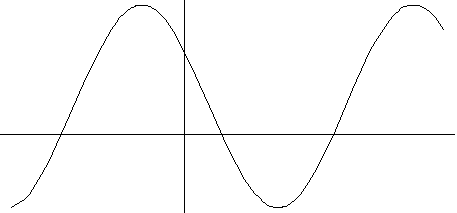
8) y=a x+ b sinx+c cosx
a>0 a<0
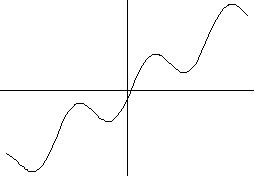
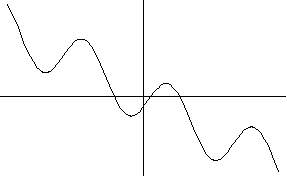
9) y=a arctgx +b
a>0 a<0
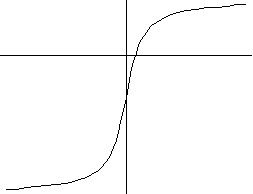
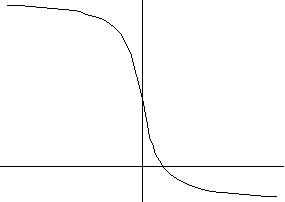
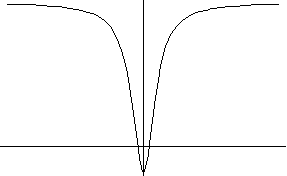
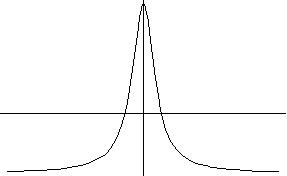
10) y=a x2/(x2+1)+b
a>0 a<0
 2015-05-20
2015-05-20 434
434








