2015-05-20
650
Пусть СМО характеризуется:
- неоднородным потоком Эрланга k -го порядка (заявки 1-го и 2-го родов);
- отказами при постановке заявок в очередь;
- ограниченным пребыванием заявок в очереди;
- дисциплиной обслуживания, когда заявка поступает в свободный канал в порядке очереди (если каналы освобождаются одновременно – то очередная заявка поступает в канал с меньшим номером);
- временем обслуживания заявок, подчиняющемуся нормальному закону распределения (различные параметры законов распределения для заявок 1-го и 2-го рода).
Поступающие заявки либо встают в очередь на обслуживание, либо получают отказ. При этом решение вопроса о постановке в очередь или отказе в обслуживании зависит от длины очереди на обслуживание. Вероятность отказа считается пропорциональной длине очереди и определяется соотношением
P отк = n / n макс,
где n и n макс – соответственно текущая и максимально допустимая длина очереди.
Как следует из приведенного соотношения, при n = n макс постановка в очередь невозможна, а при n = 0 заявка не может получить отказа.
Итак, поток заявок рассматривается как неоднородный поток (заявки 1-го и 2-го родов) с промежутками (интервалами) времени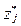 
между моментами времен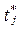и 
и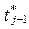 
поступления в систему двух соседних заявок.
| Номер заявки, j | … | j | … | n -1 | n | ||
Моменты времени поступления заявок,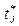 
| 
| 
| … |
| … | 
| 
|
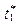
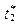
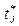
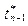
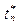
Признак заявки,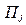 
| 
| 
| … |
| … | 
| 
|
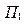
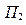
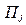
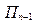
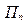
Примечание.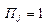 
– j -я заявка 1-го рода, 
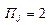– j -я заявка 2-го рода
Необходимо:
- вычислить величину интервалов времени между заявками
| Номер заявки, j | … | j | … | n | |
Интервалы времени
между заявками,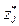 
| 
| 
| 
|
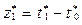
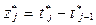
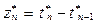
Примечание.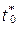 
– начало отсчета времени
- вычислить оценки математического ожидания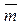 
и дисперсии 
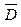интервалов времени 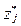между заявками в потоке;
- определить порядок потока Эрланга, на который заменяется реальный поток
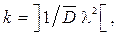
где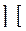 
– ближайшее целое число, а 
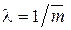– интенсивность потока заявок;
- вычислить функцию плотности распределения для первого интервала потока Эрланга (по формуле Пальма)
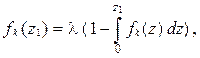
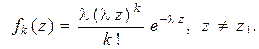
- вычислить значения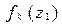 
с шагом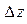 
| 
| 
|
| ||
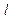
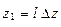
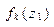
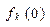
| Dz |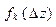 
| |
| 2Dz |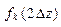 
| |
| ... | ... | ... |
|
| 
| 
|
| ... | ... | ... |
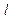
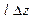
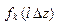
Здесь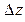 
– дискретность (интервал) изменения 
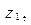выбираемая из условия обеспечения необходимой точности вычисления 
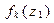; l – порядковый номер интервала
- оценить погрешность вычисления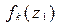 
методом трапеций
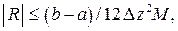
где a и b – соответственно нижний и верхний пределы интегрирования (в данном случае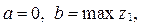 
а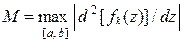 
);
- получить аналитическое выражение для функции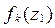 
;
- построить графики функци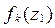й и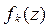 
;
- получить значения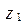 
в соответствии с функцией плотности распределения 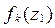, используя один из рассмотренных выше методов генерации ПСЧ с заданным законом распределения;
- получить значения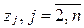 
путем просеивания простейшего потока;
- проверить по критерию c 2 распределения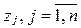 
для первого и остальных интервалов потока на соответствие распределению Эрланга k -го порядка;
- оценить вероятности поступления в СМО заявок 1-го и 2-го родов;
- построить интерфейс для ввода исходной информации для моделирования СМО и вывода результатов моделирования на дисплей и принтер.
В качестве показателей эффективности процесса функционирования СМО использовать:
– среднее время ожидания заявками обслуживания;
– среднее количество отказов для заявок 1-го и 2-го рода;
– среднее время обслуживания заявок 1-го и 2-го рода.
Таким образом, необходимо выполнить моделирование функционирования СМО:
- с неоднородным потоком Эрланга k -го порядка (заявки 1-го и 2-го рода с разными интенсивностями поступления в систему);
- с отказами при постановке заявок в очередь;
- с ограниченным пребыванием заявок в очереди;
- с дисциплиной обслуживания, когда заявка поступает в свободный канал в порядке очереди (если каналы освобождаются одновременно – то очередная заявка поступает в канал с меньшим номером);
- со временем обслуживания заявок, подчиняющемуся нормальному закону распределения (различные параметры законов распределения для заявок 1-го и 2-го рода).
