2015-05-20
377
Точность. Количество реализаций. Результаты, полученные при единичной реализации имитационной модели, носят частный характер. Для того чтобы найти адекватные оценки показателей, характеризующих свойства системы (эффективность функционирования системы), требуется многократная реализация имитационной модели с последующей статистической обработкой полученных данных.
Число требуемых реализаций N * зависит от допустимой погрешности ε и вероятности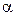 
того, что полученная величина соответствует заданному распределению. Эта связь задаётся формулой
,
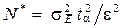где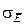 
– среднеквадратическое отклонение случайной величины, используемой в качестве показателя эффективности функционирования моделируемой системы.
Оценка среднего значения показателя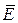 
по множеству реализаций 
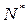определяется по формуле
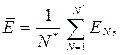
где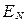 
– значение показателя эффективности, вычисленное по реализации N; 
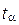–квантиль заданной вероятности 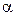для нормального распределения с математическим ожиданием 
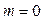и среднеквадратическим отклонением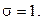 
Нормальное распределение с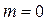 
и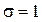 
называется каноническим нормальным распределением с функцией плотности распределения
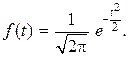
Величина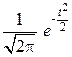 
табулирована и может быть определена из соответствующих таблиц.
Квантилем порядка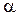 
будет такое 
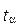, для которого 
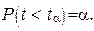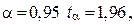Для 
а для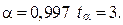 
Величина 
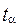определяет число среднеквадратических отклонений, которое нужно отложить вправо и влево от математического ожидания для того, чтобы вероятность попадания на полученный интервал составляла .
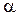Обычно дисперсия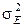 
неизвестна. В этом случае либо проводят предварительный анализ для определения оценки 
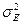, либо используют последовательный алгоритм определения необходимого объёма имитационных экспериментов.
Вначале реализуется некоторое число прогнозов N и вычисляется оценка дисперсии S 2 для показателя эффективности. Если оказывается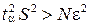 
, то выделяется дополнительное число итераций ∆N, после которых производится уточнение оценки. Таким образом, процесс повторяется далее до получения требуемой статистической точности.
Для многих встречающихся случаев процесс функционирования систем обладает свойствами стационарности и эргодичности. Это означает, что вероятностные характеристики процесса в установившемся режиме не зависят от времени. Из этого можно сделать важный для практического исследования вывод, что о свойствах системы при имитационном моделировании можно судить по одной достаточно длинной реализации.
При этом показатели эффективности находятся как средние по времени для одной реализации.
С достаточной для практических целей точностью длину реализации T можно определить, пользуясь следующим соотношением
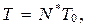
где T 0 – наблюдаемый период функционирования системы.
