Вопрос: Уравнение задачи синтеза оптимальных систем

Рассмотрим классическую задачу вариационного исчисления:

Функционал

.

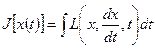Краевые условия:

,

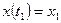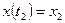
Необходимо: Найти функционала т.е. такую функцию 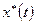при которой любая вариация 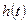только увеличивала бы значение функционала J.

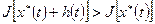при любых h(t)

Вариация- это любое такое изменение функции относительно ее первоначального значения

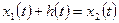
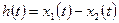
Положим, что 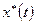функционала известна.

Введем малое такое отклонение 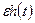( 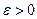малое число)

Определим значение функционала при

,

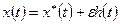
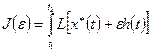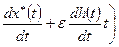
Минимум функционала достигается при 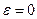т.е. функция 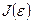имеет минимум при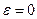

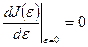
или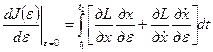

,

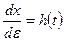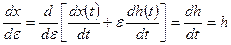
тогда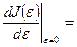

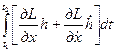
Рассмотрим второе слагаемое:

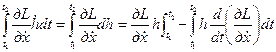
В общем получим

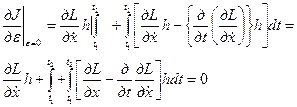
Т.к. h произвольно, то равенство следует из

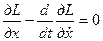, (1)

и

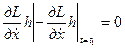(2)

Первое уравнение – это уравнение

Второе уравнение – это условие