Пример решения задачи методом динамического программирования

Предположим, что задано уравнение системы

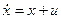
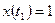
Эта задача относится к задач с незакрепленным правым концом.

Рассмотрим уравнение

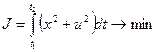
Конкретизируем уравнение Беллмана:

,

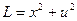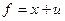
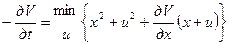
Обозначим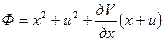

Определим экстремум выражения

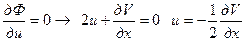
Подставляя функцию управления в уравнение Беллмана, получим

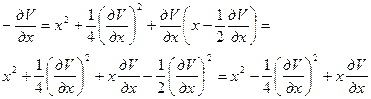
Положим 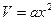из условия 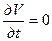следует

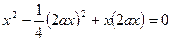
пологая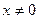

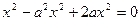
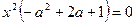
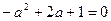или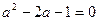

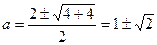
Т. о 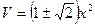, откуда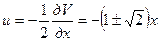

Возможны два типа уравнений

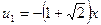
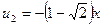
Две оптимальные траектории

,

,

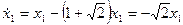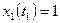
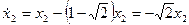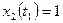
Каждая из них обеспечивает экстремум для J

Для выбора 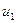или 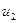используют дополнительные признаки. Например, устойчивость системы.

Движение 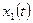устойчиво (Почему?)

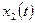неустойчиво (Почему?)

Поэтому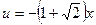

Структурная схема системы с оптимальным управлением

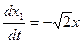
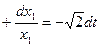
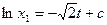
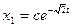
Т.о. управление, синтезированное на методе динамического программирования является замкнутым и реагирует принцип ОС.