Критерий подобия по вязкости

Пусть тело обтекается потоком жидкости, существенное свойство которой – вязкость. Возникающие при движении такой жидкости силы так называемого вязкого трения определяются по формуле Ньютона, выражающей закон внутреннего трения в жидкости:

,

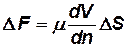(3.1)

где 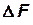– величина силы трения, действующей на элементар­ную площадку ;

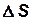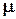– динамический коэффициент вязкости;

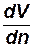– градиент скорости по нормали к рассматриваемой элементарной площадке .

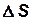Если существует динамическое подобие, то согласно выражению (2.13) отношение величин сил трения, действующих на любые соответственные площадки в соответственные моменты времени, будет одинаково и равно масштабу сил :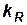

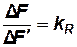
или согласно формулам (3.1) и (2.14)

.

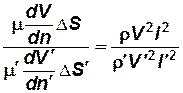Из геометрического и кинематического подобий следует, что

, .

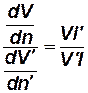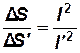Выполнив такую замену в предыдущем равенстве, находим

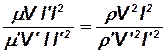
или

.

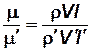(3.2)

Отсюда получаем равенство безразмерных комбина­ций для двух подобных явлений в соответственных точках:

.

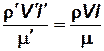Безразмерная комбинация 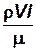называется числом Рейнольдса

.

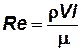(3.3)

Итак,при соблюдении подобия по вязкости жидкости числа Рейнольдса в соответственных точках потоков одинаковы:

.

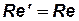Таким образом, необходимое условие подобия по вяз­кости жидкости есть равенство чисел Рейнольдса, под­считанных по определяющим данное явление параметрам:

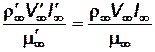
или

.

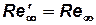(3.4)

Число 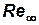– это критерий подобия по вязкости жидкости.

Критерий подобия по вязкости жидкости необходимо выдерживать при изучении явлений двух типов: при определении сил трения и при исследовании явлений, в которых вязкость принципиально изменяет картину течения (отрыв потока, взаимодействие скачков уплотнения с пограничным слоем и т.п.). Рассмотрим некоторые из этих явлений.

3.1.1. Определение сил трения на плоской пластине

Сила трения на плоской пластине находится по формуле

^,

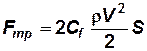где 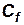– коэффициент трения, 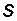– площадь пластины.

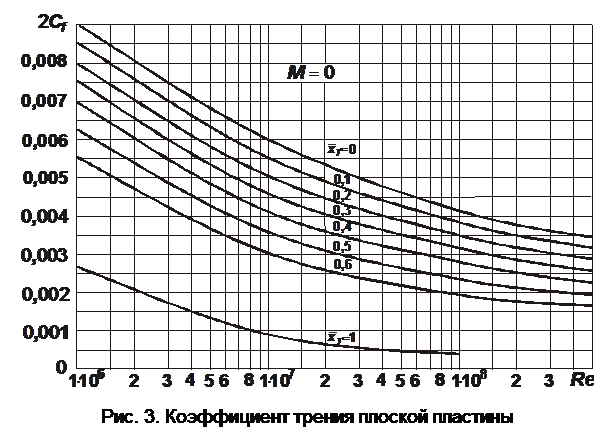На рис. 3. изображены графики для определения коэффициента .

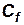Приведенные зависимости показывают, что коэффициент трения пластины зависит от числа Рейнольдса и относительного положения точки перехода ламинарного пограничного слоя в турбулентный 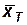. Параметр 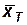определяется формулой

,

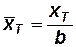где 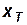– координата точки перехода ламинарного пограничного слоя в турбулентный, 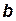– хорда пластины.

Из рис. 3 видно, что при числах Рейнольдса 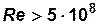коэффициент трения не зависит от числа 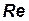(режим автомодельности). Начиная с этих чисел 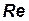равенство указанных чисел в опыте и натурном явлении выдерживать не обязательно.

Методика определения силы трения на отдельных частях летательного аппарата заключается в том, что силу трения вычисляют на эквивалентной плоской пластине, а затем полученную силу умножают на поправочные коэффициенты, учитывающие отличие в обтекании пластины и рассматриваемой части самолёта. Таким образом, и в этом случае число Рейнольдса является важнейшим критерием подобия, определяющим силы трения на летательных аппаратах.