2015-05-10
2915
При проверке согласия необходимо выполнить условие, состоящее в том, что в каждом кармане (в каждом интервале группировки) должно быть не менее 5 элементов выборки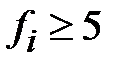 
для теоретических значений распределения частот.
Скопируете таблицу Карман – Частота на свободное место листа Excel.
Объедините (просуммируйте) верхние ячейки и нижние ячейки, содержащие теоретические частоты так, чтобы в них было величина не меньше пяти.
В рассматриваемом примере объединены (просуммированы) верхние три ячейки и нижние три ячейки, содержащие теоретические частоты так, чтобы в них была величина частоты не меньше пяти, как показано на рис. 21.
0,402347+1,672973+5,19471=7,270029
6,581834+2,38647+0,657984=9626288
Рис. 21. Таблица с объединенными тремя верхними и тремя нижними ячейками столбца теоретических частот.
Просуммируйте те же три верхние и три нижние ячейки для эмпирических частот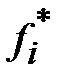 
, как показано на рис. 22.
Рис. 22. Таблица распределения эмпирических и теоретических частот подготовленная к вычислению критерия хи-квадрат Пирсона
В нижних ячейках обоих столбцов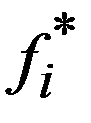 
и 
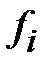вычислены суммы эмпирических и теоретических частот (
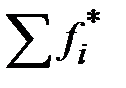и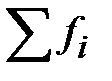 
), которые должны равняться объему выборки N = 53
Критерий хи-квадрат Пирсона состоит в оценки близости эмпирических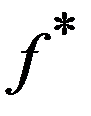 
и теоретических 
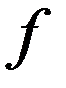частот.
Критерий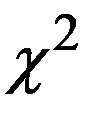 
представляет собой сумму отношений квадратов расхождений (разностей) 
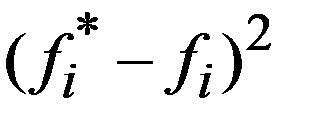к теоретическим частотам 
:
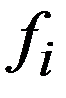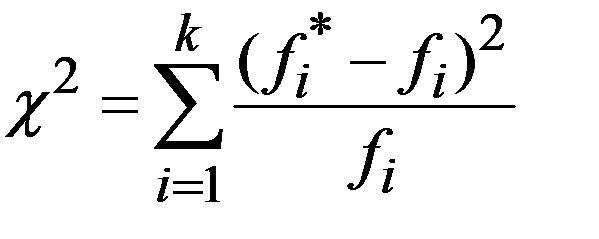
Вычисленное значение статистики 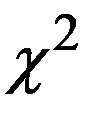сравнивается с критическим значением 
.
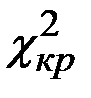Критическое значение статистики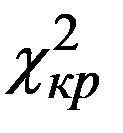 
для заданного уровня значимости 
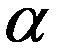и числа степеней свободы 
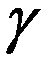(ню) определяется в Excel при помощи функции ХИ2ОБР.
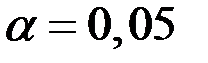- вероятность отклонить правильную гипотезу о законе распределения, уровень значимости
- число степеней свободы вычисляется по формуле:
= число группировок – 1 – число параметров эмпирического распределения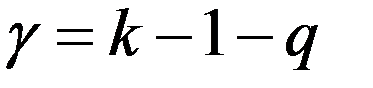 
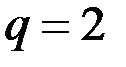– число параметров эмпирического распределения (для нормального распределения два параметра: 
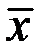- среднее значение и 
- среднее квадратическое отклонение)
Если оказывается, что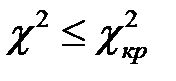 
, то принимается гипотеза о соответствии (согласии) эмпирических данных нормальному распределению.
Если оказывается, что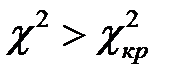 
, то гипотеза о нормальном распределении эмпирических данных отклоняется.
Вычислите в Excel критическое значение статистики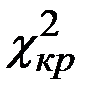 
, используя функцию ХИ2ОБР.
Вызовите функцию ХИ2ОБР: Мастер функций → Статистические → ХИ2ОБР
В диалоговом окне ХИ2ОБР заполните поля ввода данных:
Вероятность: 0,05 (уровень значимости);
Степени свободы: 2. OK!
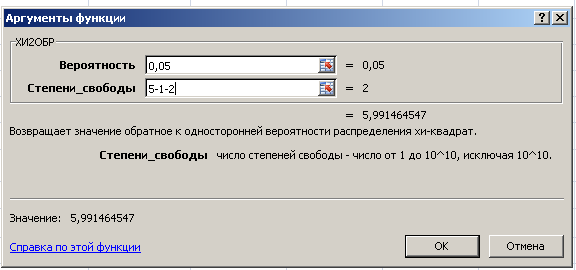
Рис. 23. Диалоговое окно функции ХИ2ОБР
Рис. 24. Результат вычисления функции ХИ2ОБР в ячейке, выделенной курсором.
Размножьте полученный результат на весь столбец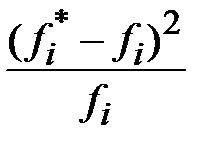 
и просуммируйте полеченные результаты. 
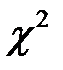= 1,25908
Рис. 25. Таблица результатами вычисления критерия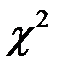 
и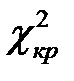 
.
Оказалось, что 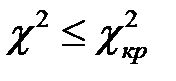, следовательно, гипотеза о соответствии (согласии) эмпирических данных нормальному распределению принимается.
