Адиабатический процесс

ЛАБОРАТОРНАЯ РАБОТА № 179

ПОЛИТРОПИЧЕСКИЙ ПРОЦЕСС

Ознакомьтесь с теорией в конспекте и учебнике (Савельев, т. 1, § 82, 97). Запустите программу. Выберите «Термодинамика и молекулярная физика», «Адиабатический процесс». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите необходимое в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.

ЦЕЛЬ РАБОТЫ:

* Знакомство с компьютерной моделью, описывающей адиабатический процесс в идеальном газе.

* Экспериментальное подтверждение закономерностей адиабатического процесса.

* Экспериментальное определение показателя адиабаты, количества степеней свободы и структуры молекул газа в данной модели.

* Ознакомление с основами анализа и моделирования термодинамических процессов в идеальных газах.

* Определение молярной теплоемкости в политропических процессах идеального газа.

* Определение показателя адиабаты и работы газа в политропическом процессе.

* КРАТКАЯ ТЕОРИЯ:

* СОСТОЯНИЕ системы имеет фиксированные значения макроскопических параметров, описывающих систему в целом. Параметры, характеризующие систему в целом, называются ПАРАМЕТРАМИ СОСТОЯНИЯ. Примерами являются температура, давление, объем и т. д.

* РАВНОВЕСНЫМ называется такое состояние системы, при котором все параметры системы имеют определенные значения, остающееся неизменными сколь угодно долго при неизменных внешних условиях.

* ОБРАТИМЫМ называется процесс, при реализации которого в обратном направлении система проходит через те же состояния, что и при прямом ходе, но в обратной последовательности. Равновесные процессы всегда обратимы.

* КРУГОВЫМ процессом (ЦИКЛОМ) называется процесс, при котором система после ряда изменений возвращается в исходное состояние.

* УРАВНЕНИЕ СОСТОЯНИЯ идеального газа (уравнение Менделеева–Клапейрона)

* .

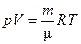* ТЕПЛОЕМКОСТЬ тела численно равна отношению количества тепла ∂ Q, сообщенного телу, к изменению температуры тела dT, которое при этом произошло:

* С _ТЕЛА = .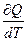

* УДЕЛЬНОЙ теплоемкостью вещества называется отношение теплоемкости к массе тела.

* Если тело не меняет свой объем, то оно не совершает работы, поэтому при постоянном объеме тела переданное телу тепло ∂ Q идет на изменение его внутренней энергии dU.

* ТЕПЛОЕМКОСТЬ ПРИ ПОСТОЯННОМ ОБЪЕМЕ:

* С _V = .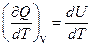

* ТЕПЛОЕМКОСТЬ ПРИ ПОСТОЯННОМ ДАВЛЕНИИ идеального газа, молекулы которого имеют i степеней свободы

* C _P = 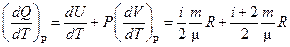(1).

* ОТНОШЕНИЕ 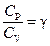является константой (в определенном диапазоне температур) для данного газа. Эта константа называется показателем адиабаты.

* Формула 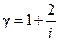(2) устанавливает связь отношения теплоемкостей g с числом степеней свободы молекулы газа i.

* ЧИСЛО (количество) СТЕПЕНЕЙ СВОБОДЫ есть минимальное количество независимых координат, необходимых для однозначного описания положения молекулы в пространстве ИЛИ минимальное количество независимых движений, суперпозиция которых дает любое движение молекулы.

* ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ всегда дает 3 степени свободы.

* ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ дает 2 степени свободы для линейной молекулы и 3 степени свободы, если атомы в молекуле не расположены на одной линии.

* КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ дает 2 n _КОЛ степеней свободы, где n _КОЛ – количество независимых колебаний атомов в молекуле (у двухатомной молекулы n _КОЛ = 1).

* АДИАБАТИЧЕСКИМ называется процесс, происходящий без теплообмена с внешней средой (∂ Q = 0). Уравнение адиабаты:

* PV ^g = const (3).

* Принято также выделять ИЗОТЕРМИЧЕСКИЙ, ИЗОБАРИЧЕСКИЙ и ИЗОХОРИЧЕСКИЙ процессы.

* ПОЛИТРОПНЫМ называется процесс, в котором молярная теплоемкость С остается постоянной. Уравнение политропического процесса имеет вид:

* рV ⁿ = const, (1)

* где n = 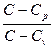. (2)

* МОЛЯРНОЙ ТЕПЛОЕМКОСТЬЮ называется физическая величина С, численно равная теплоте 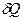, которую нужно сообщить одному молю вещества для изменения его температуры на 1 К в рассматриваемом термодинамическом процессе:

* С = 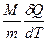, (3)

* где M – молярная масса, m – масса газа.

* Выражение (3) теперь можно записать в форме

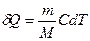* . (4)

* или в интегральной форме .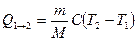

* Таким образом, если количество тепла, полученное в некотором термодинамическом процессе 1®2 при m = const, прямо пропорционально разности температур 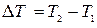, то теплоемкость газа постоянна и процесс является политропическим.

* .

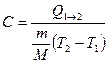* ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ для любого равновесного процесса изменения состояния идеального газа имеет вид

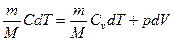* . (5)

* Тогда из уравнения (5) имеем: C = C_v + 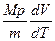. (6)

* Связь между объемом газа и его температурой в политропном процессе можно найти из выражения (1) и уравнения Клапейрона–Менделеева

* :

*

* .

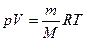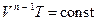* Дифференцируя последнее выражение, получим:

*

* ,

*

* .

*

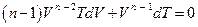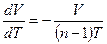* Тогда уравнение (6) примет вид:

* .

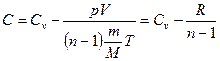* Учитывая, что 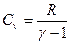, где 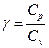– показатель адиабаты, получим:

* ,

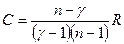* или 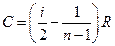. (7)

* Таким образом, если термодинамический процесс идеального газа действительно является политропным, то есть молярная теплоемкость в ходе процесса не изменяется, то ее величина рассчитывается по формуле (7).

* В настоящей работе используется модель одноатомного газа (i = 3), поэтому в политропных процессах при n = -1 согласно выражению (7) молярная теплоемкость С должна быть равна 16,6 Дж/моль×К, а при n = -2 C = 15,2 Дж/моль×К.

* Частными случаями политропного процесса являются:

* изотермический: n = 1, C = ± ¥;

* изобарический: n = 0, C = C _p;

* изохорический: n = ±¥, С = С _v;

* адиабатический: n = g, где g = 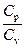, С = 0.

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

Внимательно рассмотрите картинку на рисунке, найдите рисунок элемента, в котором реализуется адиабатический процесс, обратите внимание на его теплоизоляцию. Найдите математическую формулировку условия теплоизоляции. Ознакомьтесь с графиками в правой части изображения.

Зарисуйте необходимое в свой конспект лабораторной работы.