ЛАБОРАТОРНАЯ РАБОТА №1
ПАРНОЕ ЛИНЕЙНОЕ УРАВНЕНИЕ РЕГРЕССИИ
Цель работы: рассчитать параметры парного линейного уравнения регрессии с помощью Excel, а также проанализировать качество построенной модели, используя коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.
ТЕОРИЯ
Одним из простейших уравнений регрессии, которое используется в эконометрике, является линейное уравнение:
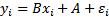 (1)
(1)
где 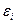 – случайная величина, называемая возмущением или случайным (остаточным) членом. Слагаемое
– случайная величина, называемая возмущением или случайным (остаточным) членом. Слагаемое 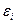 вводится в уравнение регрессии для отражения того факта, что реальные значения зависимой переменной не всегда совпадают с ее условным математическим ожиданием и могут быть различными при одном и том же значении объясняющей переменной, что отражает влияние случайных, неучтенных факторов. Таким образом, не следует ожидать получения точного соотношения между какими–либо двумя экономическими показателями, за исключением тех случаев, когда оно существует по определению.
вводится в уравнение регрессии для отражения того факта, что реальные значения зависимой переменной не всегда совпадают с ее условным математическим ожиданием и могут быть различными при одном и том же значении объясняющей переменной, что отражает влияние случайных, неучтенных факторов. Таким образом, не следует ожидать получения точного соотношения между какими–либо двумя экономическими показателями, за исключением тех случаев, когда оно существует по определению.
Существует несколько причин появления случайного фактора:
1) невключение объясняющих переменных. Соотношение между переменными 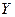 и
и 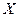 почти наверняка является большим упрощением. В действительности существуют и другие факторы, влияющие на
почти наверняка является большим упрощением. В действительности существуют и другие факторы, влияющие на 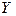 , которые не учтены в уравнении регрессии;
, которые не учтены в уравнении регрессии;
2) агрегирование переменных. Во многих случаях рассматриваемая зависимость – это попытка объединить вместе некоторое число микроэкономических соотношений. Примером является функция суммарного потребления;
3) неправильное описание структуры модели. Структура модели может быть описана неправильно или не вполне правильно. Если зависимость относится к данным о временном ряде, то значение 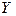 может зависеть не от фактического значения
может зависеть не от фактического значения 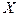 , а от значения, которое ожидалось в предыдущем периоде;
, а от значения, которое ожидалось в предыдущем периоде;
4) неправильная функциональная спецификация. Например, истинная зависимость может не являться линейной, а быть более сложной (но и она является лишь приближением);
5) ошибки измерения.
Точные значения параметров линейного уравнения регрессии (1) на практике получить невозможно. Можно только оценить 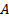 ,
, 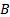 и
и 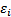 , т.е. найти уравнение вида:
, т.е. найти уравнение вида:
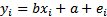 (2)
(2)
Здесь коэффициент 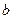 называется выборочным коэффициентом регрессии
называется выборочным коэффициентом регрессии 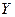 по
по 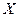 . Коэффициент регрессии
. Коэффициент регрессии 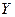 по
по 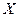 показывает, на сколько единиц в среднем изменяется переменная
показывает, на сколько единиц в среднем изменяется переменная 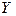 при увеличении переменной
при увеличении переменной 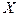 на одну единицу. Коэффициент
на одну единицу. Коэффициент 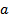 называется свободным коэффициентом. Слагаемое
называется свободным коэффициентом. Слагаемое 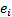 в уравнении (2) называется остатком; он равен разностью в точке
в уравнении (2) называется остатком; он равен разностью в точке 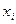 между экспериментальным и расчетным значением результативного признака, т.е.
между экспериментальным и расчетным значением результативного признака, т.е. 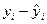 (где
(где 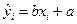 ).
).
Для оценки параметров уравнения регрессии используется ряд методов, один из которых метод наименьших квадратов (МНК).
Пусть в результате наблюдений получена таблица значений переменной 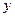 для ряда значений (независимой) переменной
для ряда значений (независимой) переменной 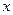 :
:
Таблица 1
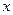 | 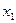 | 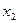 | 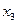 | … | 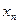 |
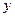 | 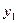 | 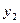 | 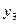 | … | 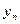 |
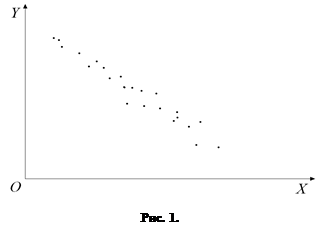
Предположим, что точки 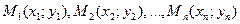 примерно располагаются на одной прямой (см. рис. 1). Это означает, что зависимость между
примерно располагаются на одной прямой (см. рис. 1). Это означает, что зависимость между 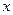 и
и 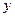 близка к линейной
близка к линейной 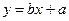 . Подберем неизвестные коэффициенты
. Подберем неизвестные коэффициенты 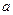 и
и 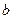 так, чтобы прямая
так, чтобы прямая 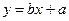 лежала по возможности ближе к каждой из нанесенных точек. Сущность МНК заключается в том, что искомую прямую
лежала по возможности ближе к каждой из нанесенных точек. Сущность МНК заключается в том, что искомую прямую 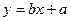 выбирают таким образом, чтобы сумма квадратов остатков
выбирают таким образом, чтобы сумма квадратов остатков 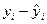 была бы наименьшей. Таким образом, неизвестные параметры
была бы наименьшей. Таким образом, неизвестные параметры 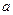 и
и 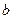 находят из условия, что сумма
находят из условия, что сумма 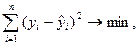 т.е.
т.е. 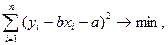 имела бы наименьшее значение. Поскольку
имела бы наименьшее значение. Поскольку 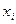 и
и  – постоянные числа (данные опыта), то указанная сумма есть функция параметров
– постоянные числа (данные опыта), то указанная сумма есть функция параметров 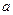 и
и 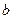 :
:
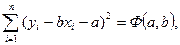 (3)
(3)
Исследуем данную функцию двух переменных на точки экстремума. Чтобы найти значения параметров 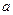 и
и 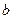 , воспользуемся необходимым условием экстремума функции нескольких переменных: найдем частные производные функции
, воспользуемся необходимым условием экстремума функции нескольких переменных: найдем частные производные функции 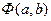 по
по 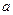 и
и 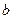 , и приравняем их к нулю:
, и приравняем их к нулю:
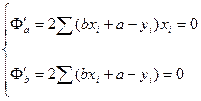 (4)
(4)
Следовательно, параметры 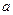 и
и 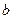 , для которых осуществляется наилучшее приближение (в указанном смысле), определяется из системы уравнений, которую можно переписать в следующем виде:
, для которых осуществляется наилучшее приближение (в указанном смысле), определяется из системы уравнений, которую можно переписать в следующем виде:
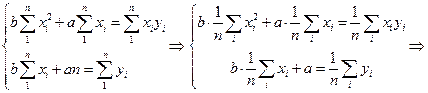
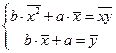 (5)
(5)
Можно доказать, что эта система всегда имеет единственное решение и что для найденных чисел 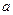 и
и 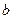 функция
функция 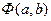 достигает минимума:
достигает минимума:
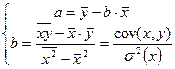 (6)
(6)
В данной формуле 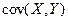 – выборочный корреляционный момент или выборочная ковариация;
– выборочный корреляционный момент или выборочная ковариация; 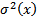 – дисперсия переменной
– дисперсия переменной 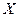 .
.
Подставляя найденные значения 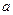 и
и 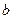 в уравнение
в уравнение 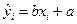 , получим линейную функцию, наилучшим образом отражающую (аппроксимирующую) зависимость между переменными
, получим линейную функцию, наилучшим образом отражающую (аппроксимирующую) зависимость между переменными 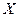 и
и 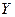 , полученную из опыта.
, полученную из опыта.
Уравнения регрессии позволяют прогнозировать возможные значения зависимых переменных. Регрессионные модели применимы для определения оптимальной области приложения усилий, например, границы, за рамки которой дальнейшее вложение капитала уже не приносит пропорционального увеличения прибыли.
Коэффициент корреляции измеряет степень и определяет направление только прямолинейных связей. Коэффициент парной корреляции 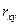 есть безразмерная величина, значения которой принадлежат отрезку:
есть безразмерная величина, значения которой принадлежат отрезку: 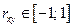 . Выборочный коэффициент парной корреляции
. Выборочный коэффициент парной корреляции 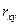 вычисляется по формуле:
вычисляется по формуле:
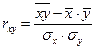 , (7)
, (7)
Соответствие между значениями 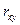 и характером связи может быть представлено следующей таблицей (таблица Чеддока):
и характером связи может быть представлено следующей таблицей (таблица Чеддока):
Значение коэффициента парной корреляции, 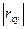 | Связь |
| Функциональная | |
| >0,9 | Очень сильная |
| 0,7 – 0,9 | Тесная (сильная) |
| 0,5 – 0,7 | Заметная |
| 0,3 – 0,5 | Умеренная |
| <0,3 | Слабая |
| Отсутствует |
Чем ближе 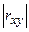 к единице, тем теснее связь между Y и X (тем ближе связь к линейной). Геометрически это означает, что чем больше по модулю коэффициент корреляции, тем ближе экспериментальные точки прилежат к линии регрессии (рис. 2).
к единице, тем теснее связь между Y и X (тем ближе связь к линейной). Геометрически это означает, что чем больше по модулю коэффициент корреляции, тем ближе экспериментальные точки прилежат к линии регрессии (рис. 2).
Проанализируем виды корреляционных полей, представленных на графиках. Очевидно, что в первом случае связь между переменными сильная, а во втором случае – слабая.
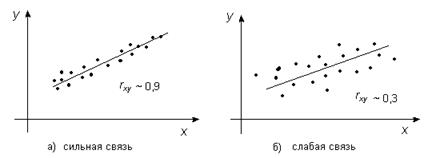
Рис. 2.
Если коэффициент корреляции положителен 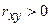 , то связь между переменными является прямой, а если
, то связь между переменными является прямой, а если 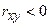 , то связь обратная (т.е. с увеличением фактора (переменной
, то связь обратная (т.е. с увеличением фактора (переменной  ) результативный признак (переменная
) результативный признак (переменная  ) будет уменьшаться) (рис. 3). Графически это будет выглядеть следующим образом:
) будет уменьшаться) (рис. 3). Графически это будет выглядеть следующим образом:
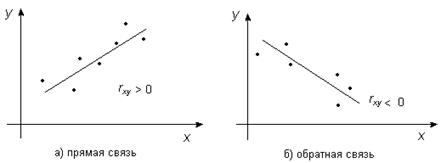
Рис. 3.
Если 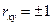 , то между величинами Y и X наблюдается функциональная зависимость, и все экспериментальные точки лежат на линии регрессии (рис. 4).
, то между величинами Y и X наблюдается функциональная зависимость, и все экспериментальные точки лежат на линии регрессии (рис. 4).
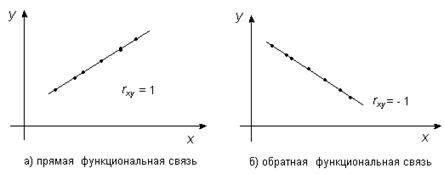
Рис. 4.
Если 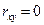 , толинейная корреляционная связь между переменными отсутствует, т.е.
, толинейная корреляционная связь между переменными отсутствует, т.е.  (см. рис. 5).
(см. рис. 5).
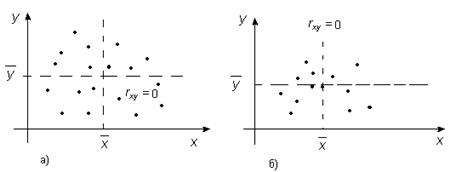
Рис. 5.
Равенство коэффициента нулю говорит лишь об отсутствии линейной связи между переменными, но при этом между ними может существовать какая-либо другая связь.
Оценку качества построенной модели (в первом приближении) дает коэффициент (индекс) детерминации и средняя ошибка аппроксимации.
Общая сумма квадратов отклонений переменной  от среднего значения
от среднего значения  раскладывается на два слагаемых: «объясненную» (факторную) и «остаточную» («необъясненную») сумму квадратов:
раскладывается на два слагаемых: «объясненную» (факторную) и «остаточную» («необъясненную») сумму квадратов:
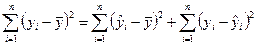 (8)
(8)
Докажем справедливость данного соотношения. Для этого преобразуем выражение общей сумы квадратов:
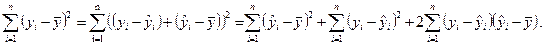
Покажем, что удвоенное произведение равно нулю.
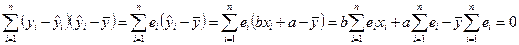 .
.
Здесь учли 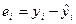 ,
, 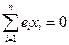 и
и 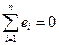 (см. систему 2).
(см. систему 2).
Общая сумма квадратов отклонений индивидуальных значений результативного признака 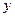 от среднего значения
от среднего значения 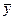 вызвана влиянием множества причин, которые можно условно разбить на две группы: изучаемые факторы и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси абсцисс и
вызвана влиянием множества причин, которые можно условно разбить на две группы: изучаемые факторы и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси абсцисс и 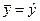 . Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадает с остаточной. Если же прочие факторы не влияют на результат, то
. Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадает с остаточной. Если же прочие факторы не влияют на результат, то 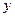 связан с
связан с 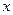 функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов. Таким образом, отношение факторной суммы квадратов к общей сумме может характеризовать качество построенной модели. Такое отношение называется коэффициентом детерминации R2:
функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов. Таким образом, отношение факторной суммы квадратов к общей сумме может характеризовать качество построенной модели. Такое отношение называется коэффициентом детерминации R2:
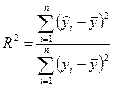 , (9)
, (9)
Коэффициент детерминации показывает, какая доля изменения (дисперсии) зависимой переменной обусловлена изменением объясняющей переменной. Например, R 2 = 0,75 – это значит, что на 75% изменение зависимой величины Y обусловлено изменением фактора X и на 25% – действием других неучтенных факторов.
Коэффициент детерминации равен квадрату коэффициента корреляции 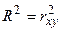 , поэтому значения
, поэтому значения 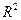 лежат в промежутке [0;1]. Чем ближе значение R2 к единице, тем лучше модель описывает экспериментальные данные, тем ближе точки прилежат к линии регрессии. Отметим, что коэффициент детерминации имеет смысл только при наличии свободного члена в уравнении регрессии.
лежат в промежутке [0;1]. Чем ближе значение R2 к единице, тем лучше модель описывает экспериментальные данные, тем ближе точки прилежат к линии регрессии. Отметим, что коэффициент детерминации имеет смысл только при наличии свободного члена в уравнении регрессии.
Помимо коэффициента детерминации о качестве модели говорит средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
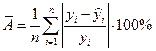 , (10)
, (10)
где 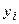 – наблюдаемое в i -том опыте значение величины Y,
– наблюдаемое в i -том опыте значение величины Y, 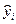 – значение, рассчитанное по уравнению регрессии для данного
– значение, рассчитанное по уравнению регрессии для данного 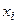 , n – число опытов. Допустимый предел значений
, n – число опытов. Допустимый предел значений  , при котором качество модели считается приемлемым, – не более 8-10%.
, при котором качество модели считается приемлемым, – не более 8-10%.
ПОСТАНОВКА ЗАДАЧИ
Для анализа зависимости объема потребления 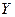 (руб.) домохозяйства в зависимости от располагаемого дохода
(руб.) домохозяйства в зависимости от располагаемого дохода 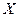 (руб.) отобрана выборка объема
(руб.) отобрана выборка объема 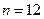 , результаты которой приведены в таблице:
, результаты которой приведены в таблице:
| № | ||||||||||||
 | ||||||||||||
 |
Необходимо:
1. найти параметры 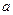 и
и 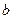 линейного уравнения парной регрессии
линейного уравнения парной регрессии 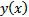 ;
;
2. найти коэффициент детерминации;
3. рассчитать линейный коэффициент парной корреляции и оценить тесноту связи, используя таблицу Чеддока;
4. Найти среднюю ошибку аппроксимации;
5. Построить график линейного уравнения регрессии.
Данную работу можно выполнить в Excel 2003 с использованием инструмента анализа данных Сервис/Анализ данных/Регрессия. При помощи данного пакета некоторые величины считаются автоматически, а некоторые необходимо рассчитать самим.
1. Откройте Excel.
2. Введите данные в виде столбцов.
3. С помощью мастера диаграмм постройте корреляционное поле и сделайте предположение о характере распределения. Ниже приведенный алгоритм построения корреляционного поля для Excel 2003.
3.1. Активизируйте Мастер диаграмм. В главном меню выберите Вставка/Диаграмма (или на панели инструментов Стандартная щелкните по кнопке Мастер диаграмм).
3.2. В появившимся окне выберите Точечная. Щелкните по кнопке Далее.
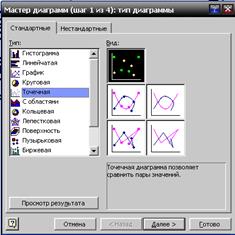
3.3. В новом диалоговом окне установите флажок размещения в столбцах (строках). Добавьте ряд. Заполните диапазон данных. Далее.
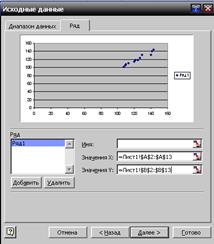
3.4. Заполните параметры диаграммы на разных закладках. Щелкните Далее.
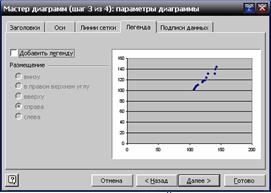
3.5. Укажите место размещения диаграммы. Нажмите Готово.
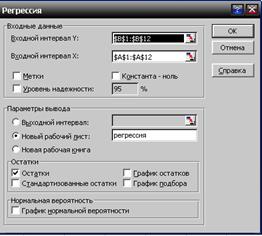
4. В главном меню выберете последовательно пункты: Сервис – Анализ данных – Регрессия. (Если в Сервисе нет Анализа данных необходимо зайти в Надстройки и установить флажок на Пакет анализа.)
5. Заполните диалоговое окно инструмента Пакета анализа Регрессия.
 2015-05-10
2015-05-10 2926
2926