СИММЕТРИЧНАЯ РЕЗИСТИВНАЯ НАГРУЗКА
Соберите схему трехфазной трехпроводной цепи, включив в каждую фазу приемника, соединенного по схеме «звезда», резистор с номинальным сопротивлением 1 кОм (рис. 6.6).
Измерьте фазные напряжения источника  ,
, 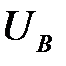 ,
, 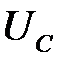 и фазные напряжения приемника
и фазные напряжения приемника 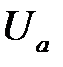 ,
,  ,
, 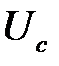 , а также линейные токи и активную мощность трехфазной цепи. В трехпроводной цепи для измерения активной мощности используется схема двух ваттметров (рис. 6.7). Подключая токовую цепь ваттметра сначала в фазу С, а цепь напряжения – на напряжение UСB, затем токовую цепь в фазу А, а цепь напряжения – на напряжение UАB, измерьте две активные мощности и вычислите суммарную
, а также линейные токи и активную мощность трехфазной цепи. В трехпроводной цепи для измерения активной мощности используется схема двух ваттметров (рис. 6.7). Подключая токовую цепь ваттметра сначала в фазу С, а цепь напряжения – на напряжение UСB, затем токовую цепь в фазу А, а цепь напряжения – на напряжение UАB, измерьте две активные мощности и вычислите суммарную
активную мощность. (Для переключения ваттметра из одной цепи в другую, также как и амперметра, используйте специальный коммутационный мини блок «амперметр» и пару проводников с коаксиальным разъёмом!). Результаты измерений занесите в табл. 6.3. Измерение напряжений на элементах схемы производите поочередным подключением вольтметра к различным участкам цепи.
По данным опыта проверьте соотношение между фазными напряжениями источника и фазными напряжениями приемника. Постройте топографическую диаграмму напряжений и векторную диаграмму токов.
Считая известными фазные напряжения источника и параметры (сопротивления) фаз приемника, рассчитайте напряжение смещения нейтрали, фазные напряжения приемника, фазные (линейные) токи, а также активные мощности приемника. Результаты расчетов занесите в табл. 6.3. Проверьте баланс активных мощностей.
Топографическая диаграмма напряжений источника не зависит от схемы соединения фаз приемника и будет иметь такой же вид, как и для четырехпроводной цепи (рис. 6.3÷6.5). Если принять потенциал точки N источника равным нулю, то при отсутствии нейтрального провода потенциал точки n приемника будет равен напряжению смещения нейтрали 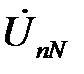 . При известных комплексных фазных напряжениях источника
. При известных комплексных фазных напряжениях источника 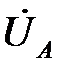 ,
, 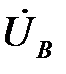 ,
, 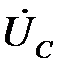 и параметрах (сопротивлениях или проводимостях) фаз
и параметрах (сопротивлениях или проводимостях) фаз
Таблица 6.3.
| Трехпроводная цепь | Симметричная резистивная нагрузка | Несимметричная резистивная нагрузка | Короткое замыкание фазы приемника | Обрыв линейного провода | |
| Измеренные фазные напряжения источника, В | UA | ||||
| UB | |||||
| UC | |||||
| Измеренные фазные напряжения приемника, В | Uа | ||||
| Ub | |||||
| Uc | |||||
| Измеренные фазные токи, мА | IA | ||||
| IB | |||||
| IC | |||||
| Измеренные мощности, мВт | Р 1 | ||||
| P2 | |||||
| SP | |||||
| Рассчитанные напряжение смещения нейтрали и фазные напряжения приемника, В | UnN | ||||
| Uа | |||||
| Ub | |||||
| Uc | |||||
| Рассчитанные фазные токи, мА | IA | ||||
| IB | |||||
| IC | |||||
| Рассчитанные мощности фаз приемника, мВт | Р А | ||||
| PВ | |||||
| PС | |||||
| SP |
приемника 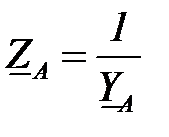 ,
,  ,
, 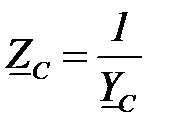 напряжение смещения нейтрали может быть определено по формуле:
напряжение смещения нейтрали может быть определено по формуле:
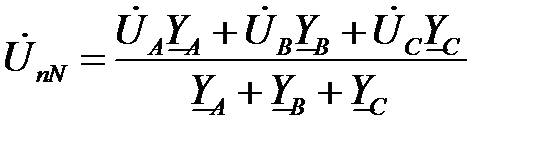 .
.
В случае симметричного приемника 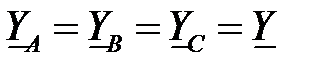 напряжение смещения нейтрали
напряжение смещения нейтрали
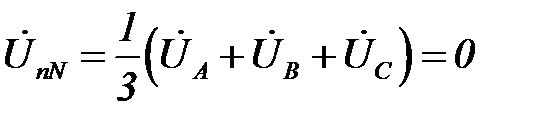 .
.
Следовательно, в случае симметричной резистивной нагрузки, когда 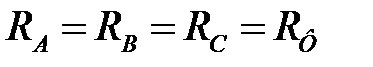 , потенциалы точек N и n будут равны, и режим работы трехпроводной трехфазной цепи ничем не будет отличаться от режима работы четырехпроводной цепи, рассмотренного ранее.
, потенциалы точек N и n будут равны, и режим работы трехпроводной трехфазной цепи ничем не будет отличаться от режима работы четырехпроводной цепи, рассмотренного ранее.
НЕСИММЕТРИЧНАЯ РЕЗИСТИВНАЯ НАГРУЗКА
Соберите схему с несимметричной резистивной нагрузкой, включив в каждую фазу звезды резистор в соответствии с заданным вариантом (номер варианта соответствует номеру бригады см. табл. 6.2). Произведите измерения токов, напряжений и активных мощностей, указанных в табл. 6.3.
По данным опыта постройте топографическую диаграмму напряжений и векторную диаграмму токов.
Считая известными фазные напряжения источника и параметры (сопротивления) фаз приемника, рассчитайте напряжение смещения нейтрали, фазные напряжения приемника, фазные (линейные) токи, а также активные мощности приемника. Результаты расчетов занесите в табл. 6.3. Проверьте баланс активных мощностей.
Построение топографической диаграммы напряжений источника производится также как и в предыдущих пунктах. Так на рис. 6.8 вектор 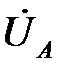 отложен по действительной оси в масштабе напряжений. В случае симметричного источника векторы напряжений
отложен по действительной оси в масштабе напряжений. В случае симметричного источника векторы напряжений 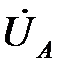 ,
, 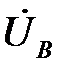 ,
, 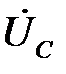 равны по величине и сдвинуты между собой на 120о. В случае трехпроводной цепи линейные напряжения источника и приемника будут соответственно равны, но фазные напряжения приемника при несимметричной нагрузке уже не будут равны фазным напряжениям источника из-за появления напряжения смещения нейтрали
равны по величине и сдвинуты между собой на 120о. В случае трехпроводной цепи линейные напряжения источника и приемника будут соответственно равны, но фазные напряжения приемника при несимметричной нагрузке уже не будут равны фазным напряжениям источника из-за появления напряжения смещения нейтрали 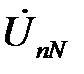 . Для нахождения потенциала точки n на комплексной плоскости по опытным данным из точек A(a), B(b) и C(c) проведите дуги окружности, равные соответственно фазным напряжениям приемника
. Для нахождения потенциала точки n на комплексной плоскости по опытным данным из точек A(a), B(b) и C(c) проведите дуги окружности, равные соответственно фазным напряжениям приемника 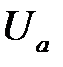 ,
,  ,
, 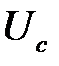 . Точка пересечения дуг определяет положение потенциала точки n (рис. 6.8).
. Точка пересечения дуг определяет положение потенциала точки n (рис. 6.8).
Векторная диаграмма токов строится в масштабе токов вместе с топографической диаграммой напряжений. При резистивной нагрузке фазные (линейные) токи
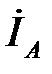 ,
, 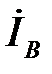 и
и 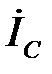 совпадают по фазе соответственно с фазными напряжениями
совпадают по фазе соответственно с фазными напряжениями 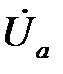 ,
, 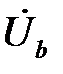 и
и 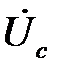 (рис. 6.8).
(рис. 6.8).
Расчетное значение напряжения смещения нейтрали 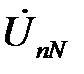 при несимметричной резистивной нагрузке определится по приведенной ранее формуле:
при несимметричной резистивной нагрузке определится по приведенной ранее формуле:
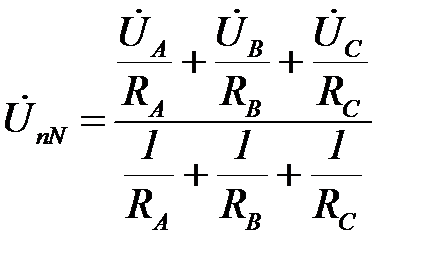 .
.
Фазные напряжения приемника 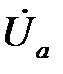 ,
, 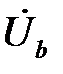 и
и 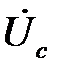 в соответствии со вторым законом Кирхгофа могут быть определены по формулам:
в соответствии со вторым законом Кирхгофа могут быть определены по формулам:
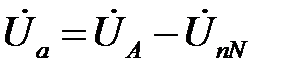 ;
; 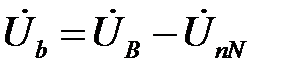 ;
; 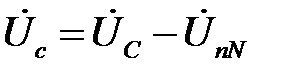 .
.
Фазные токи 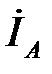 ,
, 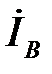 и
и 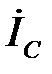 при известных фазных напряжениях
при известных фазных напряжениях 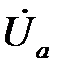 ,
, 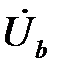 и
и 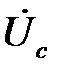 определятся по закону Ома:
определятся по закону Ома:
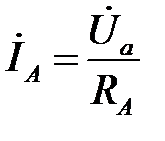 ;
; 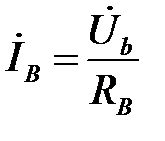 ;
; 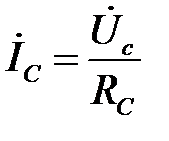 .
.
На рис. 6.8. качественно построена топографическая диаграмма напряжений и векторная диаграмма токов для случая 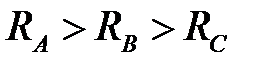 .
.
КОРОТКОЕ ЗАМЫКАНИЕ ФАЗЫ ПРИЕМНИКА
ПРИ ОДНОРОДНОЙ НАГРУЗКЕ
Восстановите схему с симметричной резистивной нагрузкой, включив в каждую фазу приемника, соединенного по схеме «звезда», резистор с номинальным сопротивлением 1 кОм (рис. 6.6). Убедитесь, что напряжения и токи в симметричном режиме совпадают со значениями, приведенными в табл. 6.3.
Закоротите одну из фаз в соответствии с заданным вариантом (номер варианта соответствует номеру бригады см. табл. 6.2). Произведите измерения токов, напряжений и активных мощностей, указанных в табл. 6.3.
По данным опыта постройте топографическую диаграмму напряжений и векторную диаграмму токов.
Считая известными фазные напряжения источника и параметры (сопротивления) фаз приемника, определите напряжение смещения нейтрали, фазные напряжения приемника, фазные (линейные) токи, а также активные мощности приемника. Результаты расчетов занесите в табл. 6.3. Проверьте баланс активных мощностей.
Построение топографической диаграммы напряжений источника производится также как и в предыдущих пунктах. При коротком замыкании одной из фаз приемника, например, фазы В, сопротивление этой фазы становится равным нулю, а проводимость – бесконечности. Потенциал нейтрали приемника n при этом будет равен потенциалу точки В источника (рис. 6.9), а фазные напряжения 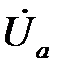 и
и 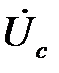 приемника равны линейным напряжениям источника:
приемника равны линейным напряжениям источника:
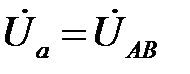 ;
; 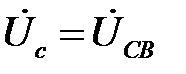 .
.
Напряжение смещения нейтрали будет равно фазному напряжению источника
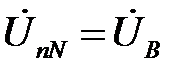 . Формально последнее выражение может быть получено из общей формулы определения
. Формально последнее выражение может быть получено из общей формулы определения 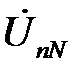 , если положить
, если положить 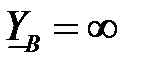 и применить правило Лопиталя.
и применить правило Лопиталя.
Поскольку при коротком замыкании фазы В приемника действующие значения фазных напряжений 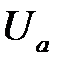 и
и 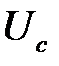 возрастут в
возрастут в 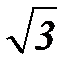 раз, то во столько же возрастут значения и токов этих фаз. Значение тока в фазе В, в которой произошло короткое замыкание может быть определен по первому закону Кирхгофа:
раз, то во столько же возрастут значения и токов этих фаз. Значение тока в фазе В, в которой произошло короткое замыкание может быть определен по первому закону Кирхгофа:
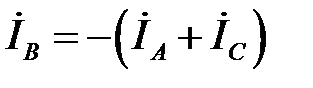 .
.
Векторная диаграмма токов для рассмотренного случая приведена на рис. 6.9. Если до аварии нагрузка в трехфазной цепи была симметричной, то после короткого замыкания ток в этой фазе возрастет в 3 раза по сравнению до аварийным режимом.
ОБРЫВ ЛИНЕЙНОГО ПРОВОДА
ПРИ ОДНОРОДНОЙ НАГРУЗКЕ
Восстановите схему с симметричной резистивной нагрузкой (рис. 6.5). Убедитесь, что напряжения и токи в симметричном режиме совпадают со значениями, приведенными в табл. 6.3.
Отключите одну из линий в соответствии с заданным вариантом (номер варианта соответствует номеру бригады см. табл. 6.2). Произведите измерения токов, напряжений и активных мощностей, указанных в табл. 6.3.
По данным опыта постройте топографическую диаграмму напряжений и векторную диаграмму токов.
Считая известными фазные напряжения источника и параметры (сопротивления) фаз приемника, определите напряжение смещения нейтрали, фазные напряжения приемника, фазные (линейные) токи, а также активные мощности приемника. Результаты расчетов занесите в табл. 6.3. Проверьте баланс активных мощностей.
При обрыве линейного провода (например, А) фазные сопротивления RB и RC оказываются соединёнными последовательно и включёнными на напряжение UВС. Цепь фактически становится однофазной. При однородной нагрузке потенциал точки n приемника сместится на линию ВС топографической диаграммы напряжений (рис. 6.10).
Построение топографической диаграммы напряжений источника производится также как и в предыдущих пунктах. При обрыве линейного провода фазы А для нахождения потенциала точки n на комплексной плоскости по опытным данным из точек B(b) и C(c) проведите дуги окружности, равные соответственно фазным напряжениям приемника  и
и 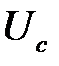 . Точка пересечения этих дуг с линией напряжения
. Точка пересечения этих дуг с линией напряжения 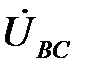 определяет положение потенциала точки n (рис. 6.10).
определяет положение потенциала точки n (рис. 6.10).
Векторная диаграмма токов строится в масштабе токов вместе с топографической диаграммой напряжений. При обрыве фазы А
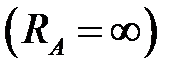 действующие значения линейных токов фаз В и С равны и при резистивной нагрузке совпадают по фазе с соответствующими фазными напряжениями приемника.
действующие значения линейных токов фаз В и С равны и при резистивной нагрузке совпадают по фазе с соответствующими фазными напряжениями приемника.
Расчетное значение напряжения смещения нейтрали 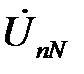 при RB=RC определится по приведенной ранее формуле:
при RB=RC определится по приведенной ранее формуле:
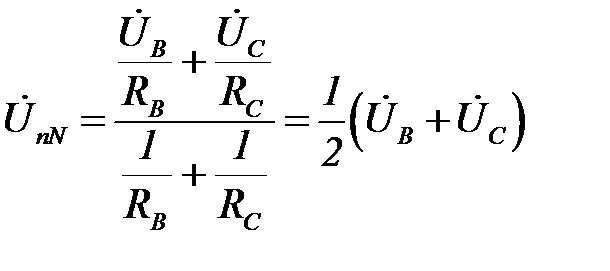 .
.
Потенциал точки n на топографической диаграмме напряжений в рассматриваемом случае может быть определен и без использования формулы между узлового напряжения. Так при обрыве фазы А и 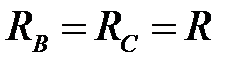
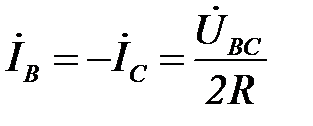 ;
; 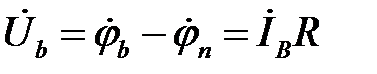 ;
; 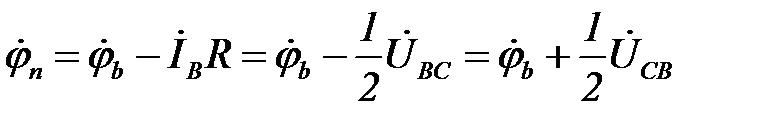 .
.
Как следует из топографической диаграммы напряжений при симметричной нагрузке и обрыве одной из фаз напряжение между точками разрыва будет равным 1,5 фазного напряжения источника (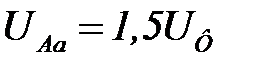 ).
).
 2015-05-10
2015-05-10 338
338







