Поле и потенциал заряженного шара

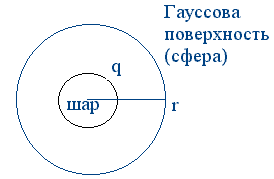
Пользуясь тем, что гауссова поверхность (в законе Гаусса) произвольная, выберем её в виде концентрической сферы, с заряженным шаром. В силу симметрии, на всей гауссовой поверхности электрическое поле будет одинаково.

Выносим его из под знака интеграла в законе Гаусса:

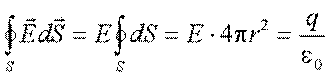То есть 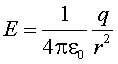- вне шара такое же поле, как от точечного заряда.

Для нахождения поля вне шара не важно, как распределён заряд внутри шара - по поверхности, или по объёму; лишь бы симметрично.

Потенциал от заряженного шара вычислим через электрическое поле, при этом удобно ноль потенциала установить на бесконечности. Общая формула для потенциала всевозможных шаров (полых, сплошных):

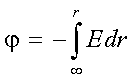
Подставляя вместо E найденные значения, получим:

· любой шар, потенциал вне шара (такой же, как от точечного заряда):

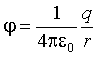
· внутри полого шара потенциал не меняется (R - радиус шара):

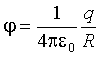
· внутри заряженного равномерно по объёму сплошного шара:

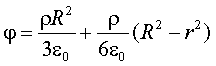
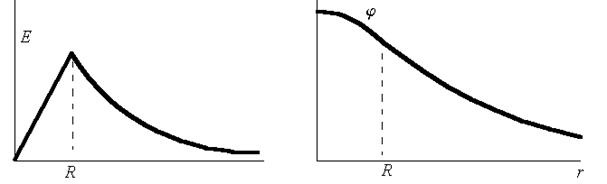
Графики полей и потенциалов имеют вид:

· Полый шар (заряд на поверхности):

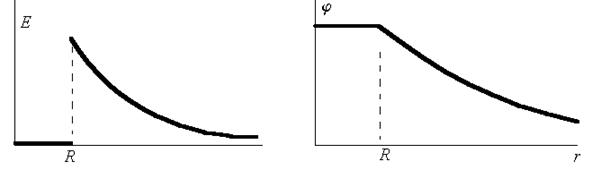
· Сплошной шар, равномерно заряженный по объёму: