Закон распределения Гаусса

Закон распределения Гаусса имеет место, когда случайная величина (например, размер после обработки, измеренный раз­мер и др.) является функцией большого числа независимых рав­нозначных факторов. Нормальное распределение имеет вид

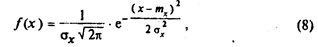
где т_x и s_х — математическое ожидание и среднее квадратическое отклонение соответственно. График плотности вероятности нормального распределения показан на рис. 3, а, а интегральная функция распределения — на рис. 3, б. Кривая распределения одномодальна и симметрична относительно вертикали, проходящей через абсциссу т_x = a₀, достигает в ней максимума. При изменении значения т_x кривая смещается вдоль оси х без изменения формы. С ростом значения s_x кривая "прижимается" к оси х, растягиваясь

вдоль нее, т.е. становится более пологой. При уменьшении s_x кривая становится более "острой", т.е. все значения х группируются вокруг значения т_х. Вероятность попадания х в заданный интервал ( a, b) при нормальном распределении легко рассчитывается с по­мощью табулированной функции Лапласа Ф (Z) (приложение 1) по формуле

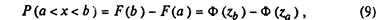
где Z_b и Z_a — аргументы функции Лапласа, Z_b = (b – т_x)/s_x. и Z_a = (а – т_x)/ s_x, а сами значения функции находят по справочным таблицам для этих аргументов. Это свойство часто используется для расчета вероятного брака при выходе за границы заданного ин­тервала, который можно рассматривать как заданное поле допуска параметра изделия.

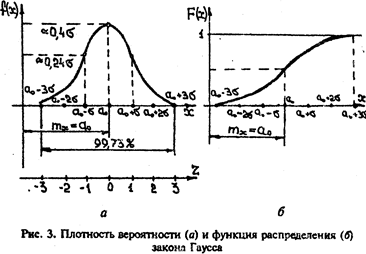
В частности, предельное отклонение для нормально распреде­ленной случайной величины Х равно ± 3 s_x или w = 6 s_x. Ана­логичные параметры распределения известны и для других за­конов распределения. Однако все они являются теоретическими (идеальными) и характеризуют генеральные совокупности слу­чайных величин. На практике эти параметры не известны, но их можно оценить по результатам наблюдений (измерений) от­дельных значений случайных величин, так или иначе выбранных из генеральной совокупности. Поэтому эти оценки называют выборочными. Их точность тем выше, чем больше объем выборки (число наблюдений).