Фирма «Фасад» производит двери для продажи местным строительным компаниям. Репутация фирмы позволяет ей продавать всю производимую продукцию. На фирме работает 10 рабочих в одну смену (8 рабочих часов), 5 дней в неделю, что дает 400 часов в неделю. Рабочее время поделено между двумя существенно различными технологическими процессами: собственно производством и конечной обработкой дверей. Из 400 рабочих часов в неделю 250 отведены под собственно производство и 150 под конечную обработку.
«Фасад» производит 3 типа дверей: стандартные, полированные и резные. В таблице 1.1 приведены временные затраты и прибыль от продажи одной двери каждого типа.
Таблица 1.1 – Затраты и прибыль от продажи дверей
| Время на производство (мин.) | Время на обработку (мин.) | Прибыль | |
| Стандартные | $ 45 | ||
| Полированные | $ 90 | ||
| Резные | $ 120 |
Задача (1). Следует подсчитать, сколько времени на каждой стадии потребуется для реализации произвольного плана производства дверей. Для стадии производства это время будет равно t1=X1*30+X2*30+X3*60 (мин), а для стадии обработки t2=X1*15+X2*30+X3*30 (мин),
По условию t1<=250*60 (мин), а t2<=150*60 (мин).
Добавим эти формулы на лист с данными задачи (таблица 1.2):
Таблица 1.2 – Формулы для табличной модели
| Фирма "Фасад" | |||||
| Время на производство (мин.) | Время на обработку (мин.) | Прибыль, $ | Переменные | ||
| Стандартные | X1 | ||||
| Полированные | X2 | ||||
| Резные | X3 | ||||
| Целевая функция | |||||
| =СУММПРОИЗВ($E$3:$E$5;B3:B5) | =СУММПРОИЗВ($E$3:$E$5;C3:C5) | =СУММПРОИЗВ(E3:E5;D3:D5) | |||
| Ограничения | =250*60 | =400*60-B8 |
Теперь имеется вся информация, необходимая надстройке «Поиск решения» для определения оптимального по прибыли плана производства.
В данном случае оказывается, что максимально возможная прибыль равна 33000 $ и получена она будет, если производить за неделю 100 полированных дверей и 200 резных. Это и есть оптимальный план производства для базовой задачи (пункт 1).
Таблица 1.3 – Оптимальный план производства для задачи (1)
| Фирма "Фасад" | |||||
| Время на производство (мин.) | Время на обработку (мин.) | Прибыль, $ | Переменные | ||
| Стандартные | X1 | ||||
| Полированные | X2 | ||||
| Резные | X3 | ||||
| Целевая функция | |||||
| Ограничения |
Задача (2). В первой части задачи мы полагали, что суммарное рабочее время по каким-то причинам (не упоминаемым в условии задачи) жестко разбито на 250 часов производства и 150 часов обработки. Возможно, что это связано со специализацией рабочих.
Тем не менее, можно попробовать выяснить, каково оптимальное распределение рабочего времени между стадиями?
Отчет по устойчивости. Чтобы получить «Отчет по устойчивости» для предыдущего решения задачи, нужно в итоговом окне Результаты поиска решения (рисунок 2.7), прежде чем нажать клавишу ОК, отметить пункт Тип отчета - Устойчивость. При этом к книге MS Excel добавится лист Отчет по устойчивости 1 (рисунок 1.4).
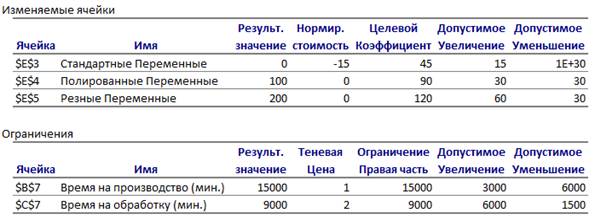
Рисунок 1.4 – Отчет по устойчивости
В данном случае нас интересует теневая цена ресурсов. Так как теневая цена Времени на обработку выше, чем Времени на производство, очевидно, что следует перераспределить рабочее время в пользу обработки. Руководствуясь отчетами об устойчивости можно подобрать нужное распределение времени, но удобнее изменить задачу.
Чтобы модифицировать задачу в соответствии с изменившимися условиями, достаточно отказаться от ограничения по рабочему времени каждой из стадий и потребовать, чтобы суммарное рабочее время не превышало = 400*60 (мин).
Оставим действующим решение задачи (1), и для модифицированной задачи создадим новый лист.
Для изменения условий добавим в ячейки D7 и D8 формулы: =С7+B7 и =400*60, соответственно. После этого нужно немного модифицировать задание надстройке «Поиск решения». Вызвав надстройку, удалим из ограничений условие $B$7:$C$7 <= $B$8:$C$8, и добавим вместо него условие D7 <= D8.
Получим следующее решение (таблица 1.5)
Таблица 1.5 – Оптимальный план производства для задачи (2)
| Фирма "Фасад" | ||||||
| Время на производство (мин.) | Время на обработку (мин.) | Прибыль, $ | Переменные | |||
| Стандартные | X1 | |||||
| Полированные | X2 | |||||
| Резные | X3 | |||||
| Целевая функция | ||||||
| Ограничения |
Распределение времени на производство и на обработку изменилось.
Кроме того отметим, во-первых, что максимальная общая прибыль выросла на 3000$ в неделю. Во-вторых, оптимальный план рекомендует выпускать только полированные двери в количестве 400 штук.
Задача (3). Новые условия, описанные в пункте 3, усложняют задачу. Чтобы их учесть следует ввести две новые переменные: количество стандартных дверей и количество полированных дверей, изготовленных из полуфабрикатов стороннего поставщика. Кроме этого нужно учесть размер заказа и потребовать безусловного его выполнения.
Организация данных на листе MS Excel в этом случае представлена на рисунке 2.11.
В ячейках G3:G5 мы подсчитываем полное количество дверей каждого типа, а в настройке «Поиска решения» сравниваем результаты с заказом. Что касается общего времени на обработку и производство, то мы вернулись к первоначальным условиям: 150 и 250 часов соответственно.
Таблица 1.6 – Оптимальный план производства для задачи (3)
| Фирма "Фасад" | |||||||
| Время на производство (мин.) | Время на обработку (мин.) | Прибыль, $ | Переменные | Всего, шт. | Заказ | ||
| Стандартные | X1 | ||||||
| Полированные | X2 | ||||||
| Резные | X3 | ||||||
| Стандартные П | X4 | ||||||
| Полированные П | X5 | ||||||
| Полное время | Целевая функция | ||||||
| Ограничения |
Задача (4). Для решения этой задачи нужно изменить только одно условие,ограничим только суммарное время двух стадий. Результат представлен на таблице 1.7.
Таблица 1.7 – Оптимальный план производства для задачи (4)
| Фирма "Фасад" | |||||||
| Время на производство (мин.) | Время на обработку (мин.) | Прибыль, $ | Переменные | Всего, шт. | Заказ | ||
| Стандартные | X1 | ||||||
| Полированные | X2 | ||||||
| Резные | X3 | ||||||
| Стандартные П | X4 | ||||||
| Полированные П | X5 | ||||||
| Полное время | Целевая функция | ||||||
| Ограничения |
Целевая функция в этом варианте задачи сильно выросла, больше чем в 1,5 раза в сравнении со случаем неоптимального разделения времени.
 2015-05-10
2015-05-10 2494
2494
