Пусть система линейных алгебраических уравнений (СЛАУ) задана в виде
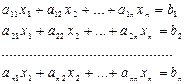 (5)
(5)
Предположим, что диагональные элементы исходной системы не равны нулю (aii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x1, второе относительно x2 и т.д. Получим следующую эквивалентную систему:
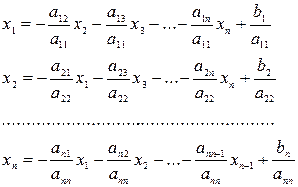 (6)
(6)
В системе (6) 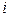 -ое уравнение представляет собой
-ое уравнение представляет собой 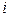 -ое уравнение системы (6), разрешённое относительно
-ое уравнение системы (6), разрешённое относительно 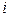 –ой неизвестной (
–ой неизвестной (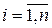 ).
).
Теперь, задав нулевое приближение 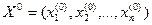 , по соотношениям (5) можем выполнять итерационный процесс. Таким образом, рабочие формулы метода простой итерации решения системы (5) будут иметь вид
, по соотношениям (5) можем выполнять итерационный процесс. Таким образом, рабочие формулы метода простой итерации решения системы (5) будут иметь вид
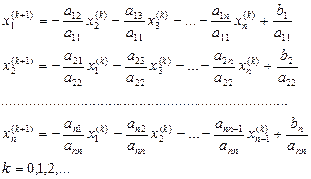 (7)
(7)
Формулы (2.3) можно записать в виде
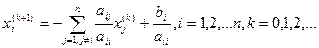 (8)
(8)
Условие окончания итерационного процесса
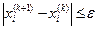 ,
, 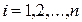 .
.
Достаточное условие сходимости. Если выполнено условие диагонального преобладания, то есть
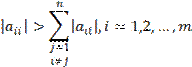
то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.
Замечание. Указанное выше условие сходимости является достаточным, т.е. если оно выполняется, то процесс сходится. Однако процесс может сходиться и при отсутствии диагонального преобладания, но может и не сойтись.
Выбор начального приближения. Компонентами нулевого приближения могут быть любые числа. Наиболее часто в качестве начального приближения берут либо свободные члены системы (5)  либо нули
либо нули 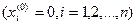 .
.
Выбор начального приближения влияет на количество итераций, необходимых для получения решения с требуемой точностью.
3. Решение системы линейных алгебраических уравнений в MathCAD
Решить СЛАУ можно следующими способами:
1. С помощью вычислительного блока Given/Find.
2. С помощью функции lsolve.
3. С помощью обратной матрицы.
Для первого способа следует использовать вычислительный блок Given/Find, состоящий из трех последовательных частей:
– Given – ключевое слово;
– система, записанная логическими операторами в виде равенств;
– Find(x1, …,xn) – встроенная функция для решения системы относительно переменных x1, …, xn.
Перед вызовом вычислительного блока всем неизвестным присвоены начальные значения. Они могут быть произвольными, т.к. решение СЛАУ с невырожденной матрицей единственно.
Для решения системы уравнений необходимо выполнить следующее:
-Задать начальное приближение для всех неизвестных, входящих в систему уравнений.
- Напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений.
- Ввести уравнения в любом порядке. Используйте [Ctrl]= для печати символа =.
- Ввести любое выражение, которое включает функцию Find, например: а:= Find (х, у).
Find (z 1, z 2 ,...)
Возвращает точное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.
На рисунке 1 показано решение системы трех линейных уравнений относительно трех неизвестных.
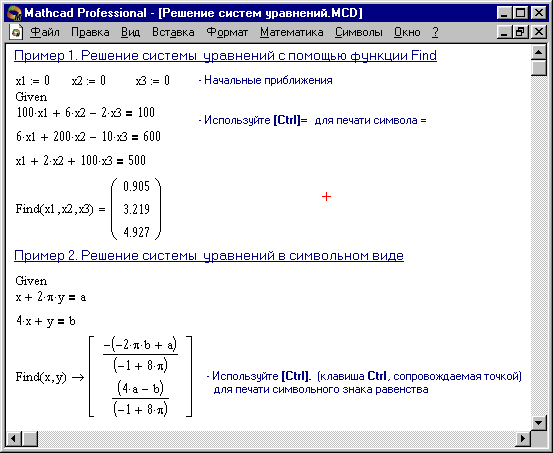
Рис. 1
2. Решение СЛАУ с помощью функции lsolve(A, b)
lsolve(A, b) – возвращает вектор х решения линейной системы уравнений Ах = b.
. Вектор b – это вектор правых частей линейной системы уравнений.
Для решения системы уравнений необходимо выполнить следующее:
-Записываем матрицу А, которая будет состоять из коэффициентов стоящих перед
неизвестными
- Аналогично записываем матрицу b, которая будет состоять из столбца свободных членов:
- решаем систему x:= lsolve(A,b).
На рисунке 4 показано решение системы трех линейных уравнений относительно трех неизвестных.
3. Решение с помощью обратной матрицы.
Если матрица А - неособенная, то есть det A 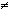 0 то система (2), или эквивалентное ей матричное уравнение (3), имеет единственное решение.
0 то система (2), или эквивалентное ей матричное уравнение (3), имеет единственное решение.
В самом деле, при условии det A 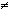 0 существует обратная матрица А -1. Умножая обе части уравнения (3) на матрицу А -1 получим:
0 существует обратная матрица А -1. Умножая обе части уравнения (3) на матрицу А -1 получим:
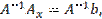
 (5)
(5)
Для решения системы уравнений необходимо выполнить следующее:
-Записать матрицу А, которая будет состоять из коэффициентов стоящих перед
Неизвестными.
- Записать матрицу b, которая будет состоять из столбца свободных членов:
- решаем систему x:= A-1b.
Вектор х содержит решениесистемы
На рисунке 2. показано решение системы трех линейных уравнений.
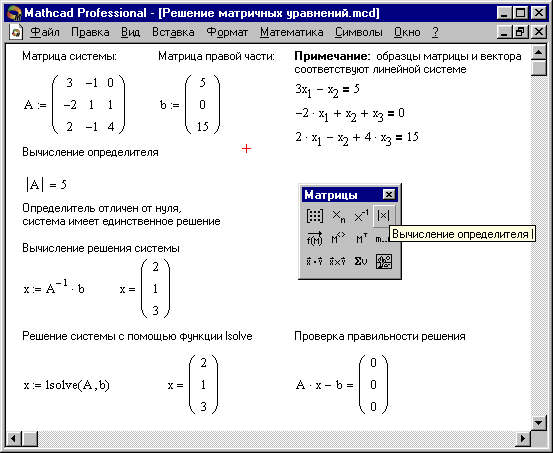
Рис. 2
Приложение 1.
Таблица 1 - Варианты индивидуальных заданий
| № варианта | Система линейных алгебраических уравнений | № варианта | Система линейных алгебраических уравнений |
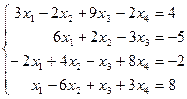 | 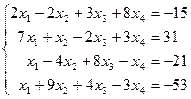 | ||
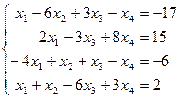 | 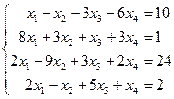 | ||
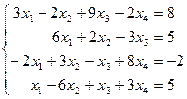 | 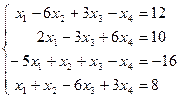 | ||
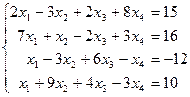 | 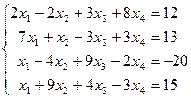 | ||
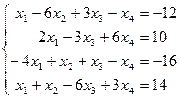 | 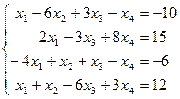 | ||
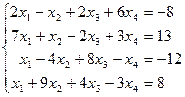 | 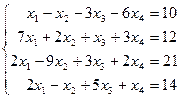 | ||
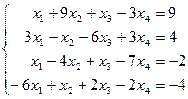 | 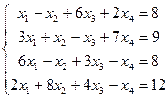 | ||
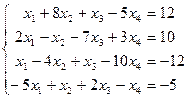 | 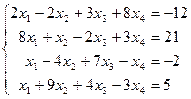 | ||
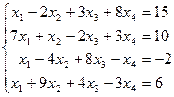 | 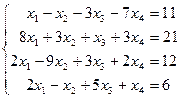 | ||
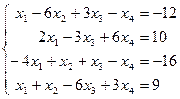 | 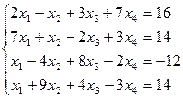 | ||
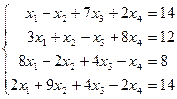 | 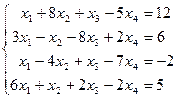 | ||
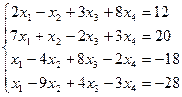 | 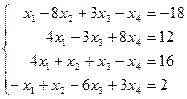 | ||
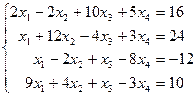 | 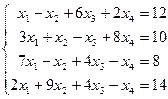 | ||
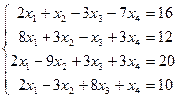 | 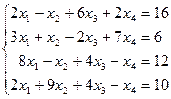 | ||
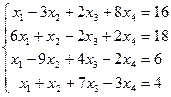 | 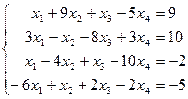 |
 2015-05-10
2015-05-10 2553
2553