ОТЧЕТ
По лабораторной работе №2
Дисциплина: Основы теории управления
Тема: Типовые соединения звеньев. Исследование систем управления с обратной связью
| Работу выполнил | ||
| студент гр. 3144/1 | Ягафаров К.И. | |
| Работу принял | ||
| доцент | Киселева Л.А. |
«__»__________2013г.
Санкт-Петербург
Последовательное соединение звеньев
1.1. Исследуем два звена, соединенных последовательно, с передаточными функциями W1(s)=K и W2(s)=1/(Ts) при К=10 и T=0,14. Передаточная функция полученной системы будет иметь следующий вид:
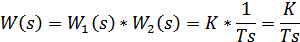
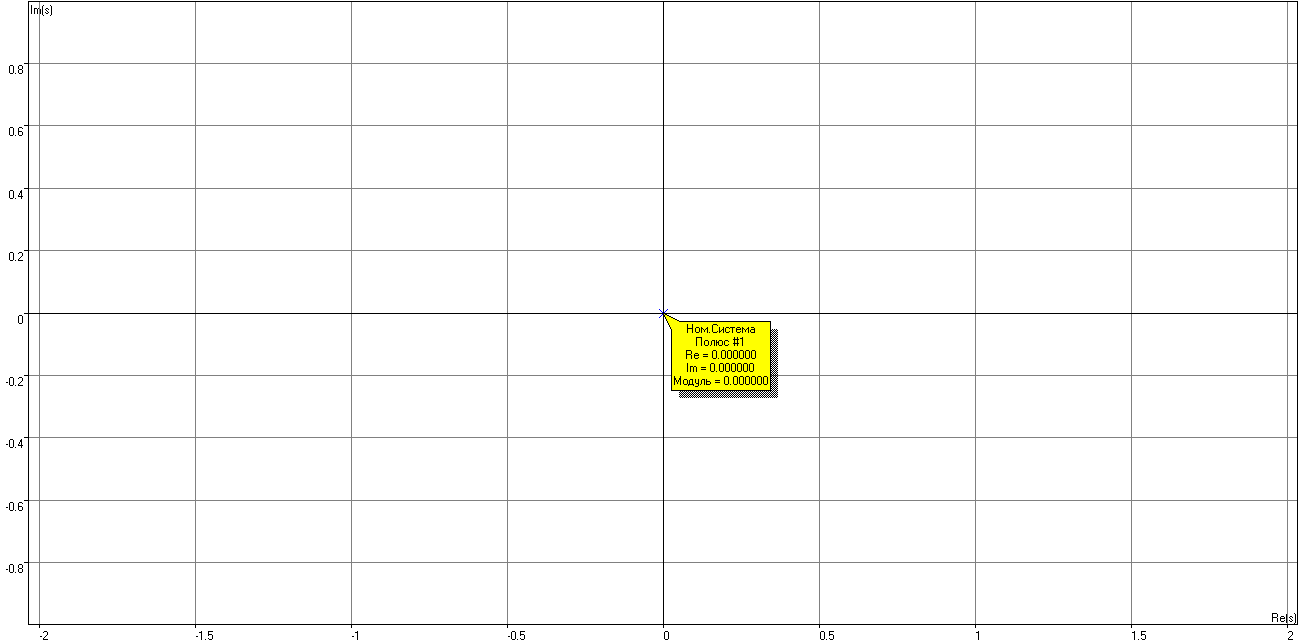
Рисунок 1 – Корневая плоскость
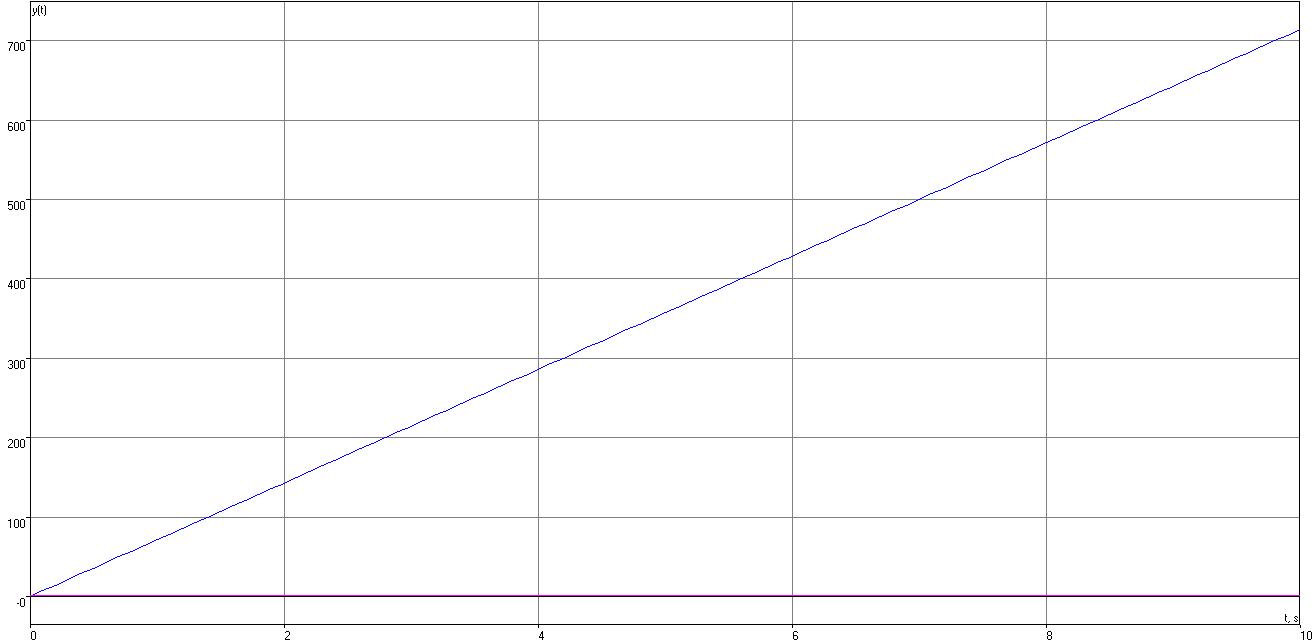 Рисунок 2 – Переходная характеристика
Рисунок 2 – Переходная характеристика
Рисунок 3 – ЛАЧХ и ЛФЧХ
1.2. Исследуем два апериодических звена, соединенных последовательно, с передаточными функциями W1(s)=K1/(1+T1s) и W2(s)=K2/(1+T2s) при К1=5, K2=10. Передаточная функция полученной системы будет иметь следующий вид:
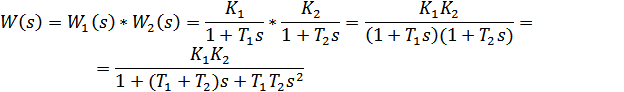
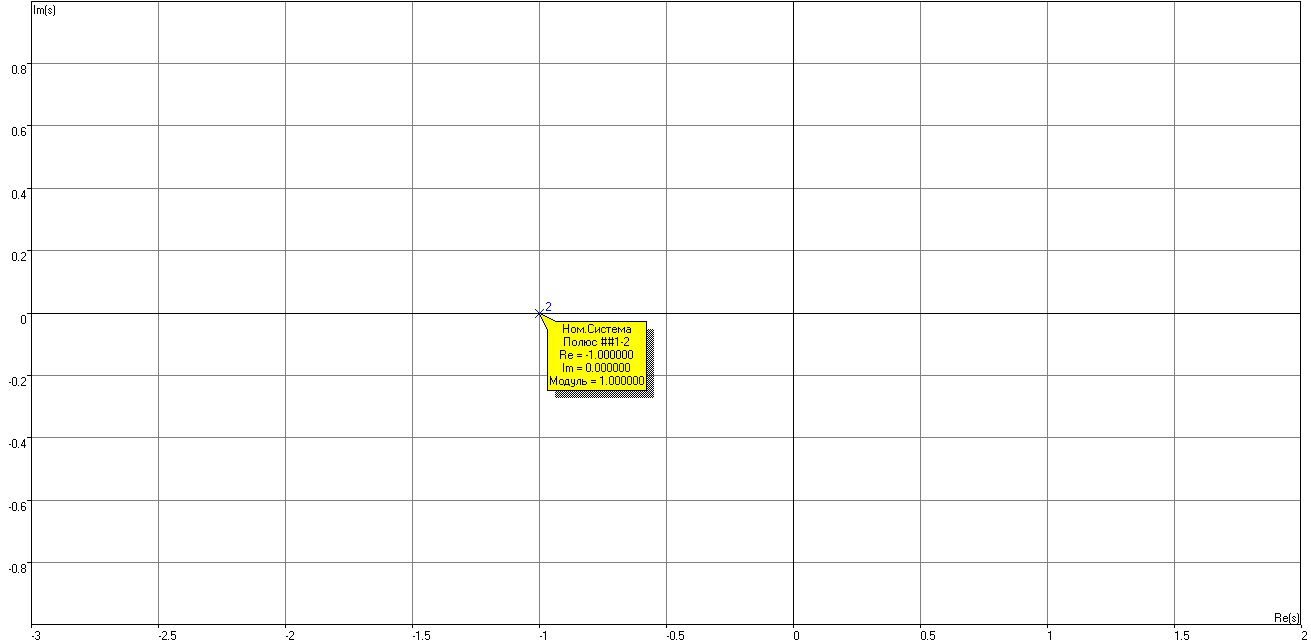
Рисунок 4 – Корневая плоскость при T1=T2=1с
Как видно из рис. 4, при одинаковых параметрах T1 и T2 полученная система имеет два совпадающих полюса с координатами (-1;0).
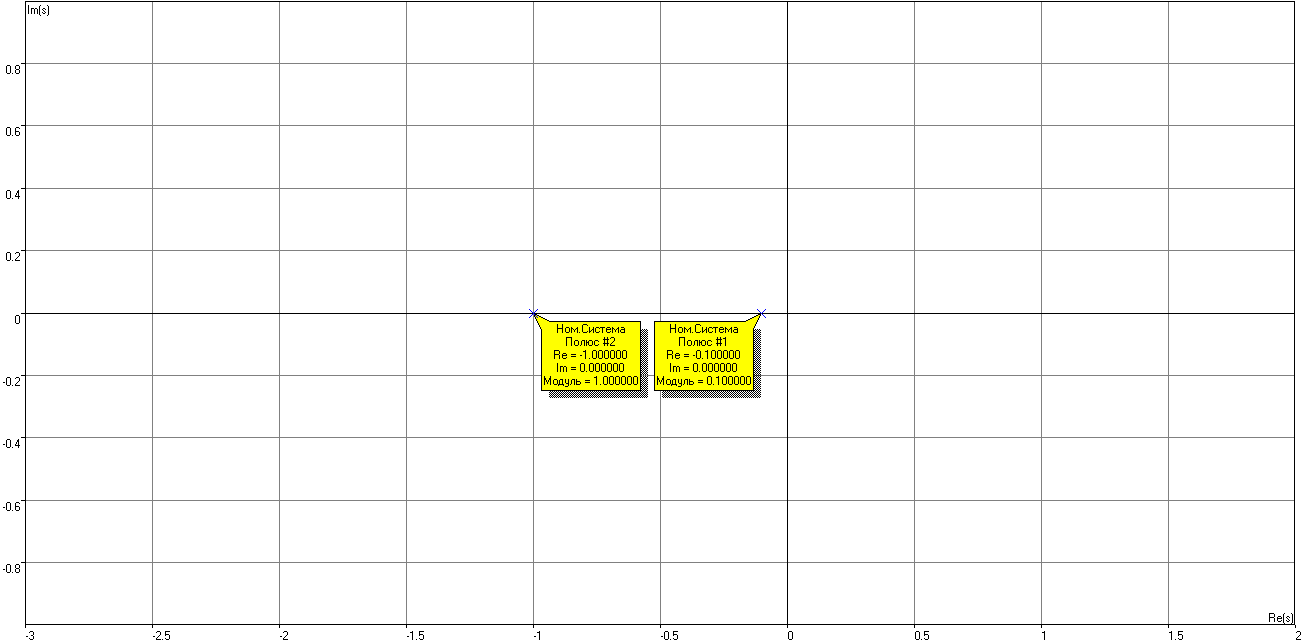
Рисунок 5 – Корневая плоскость при T1=1с, T2=10с
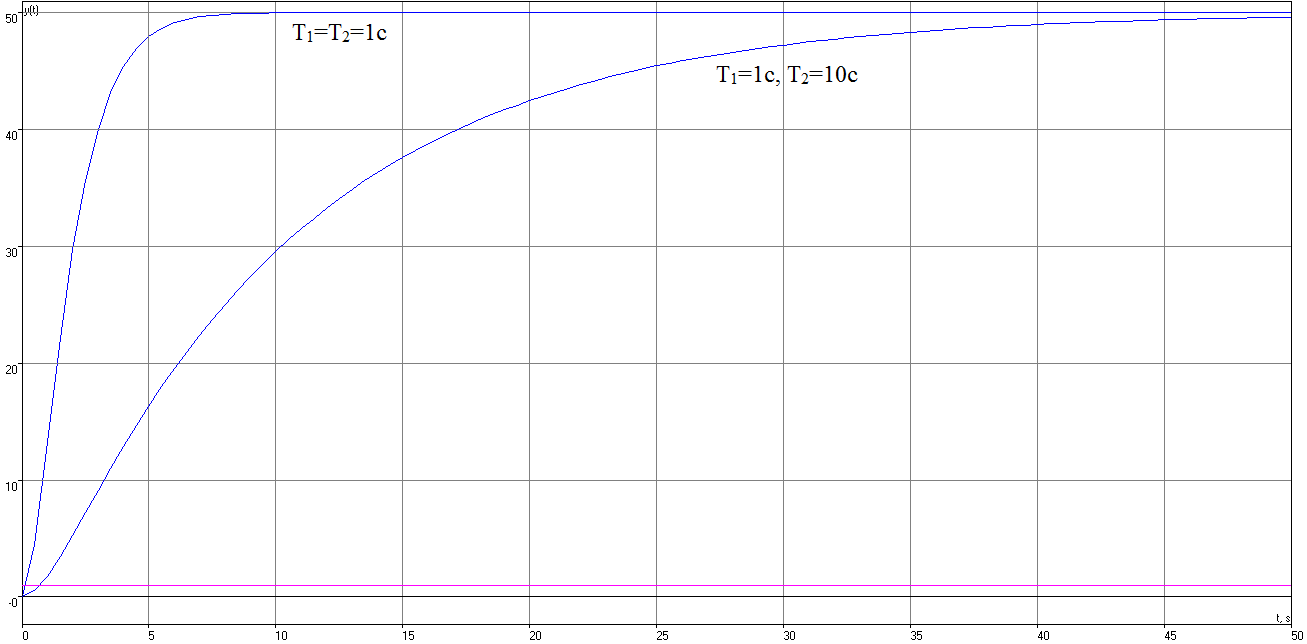
Рисунок 6 – Переходная характеристика при варьировании параметра T2
Как было написано выше, передаточная функция имеет вид:
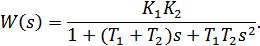
Сделав замену T1+T2=2ξT, T2=T1*T2 и K1*K2=K, получим передаточную функцию вида:
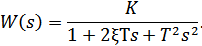
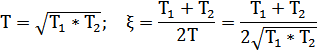
· при T1=T2=1с ξ=1;
· при T1=1с, T2=10с ξ=1,658,
т.е. полученная система соответствует апериодическому звену 2-го порядка.
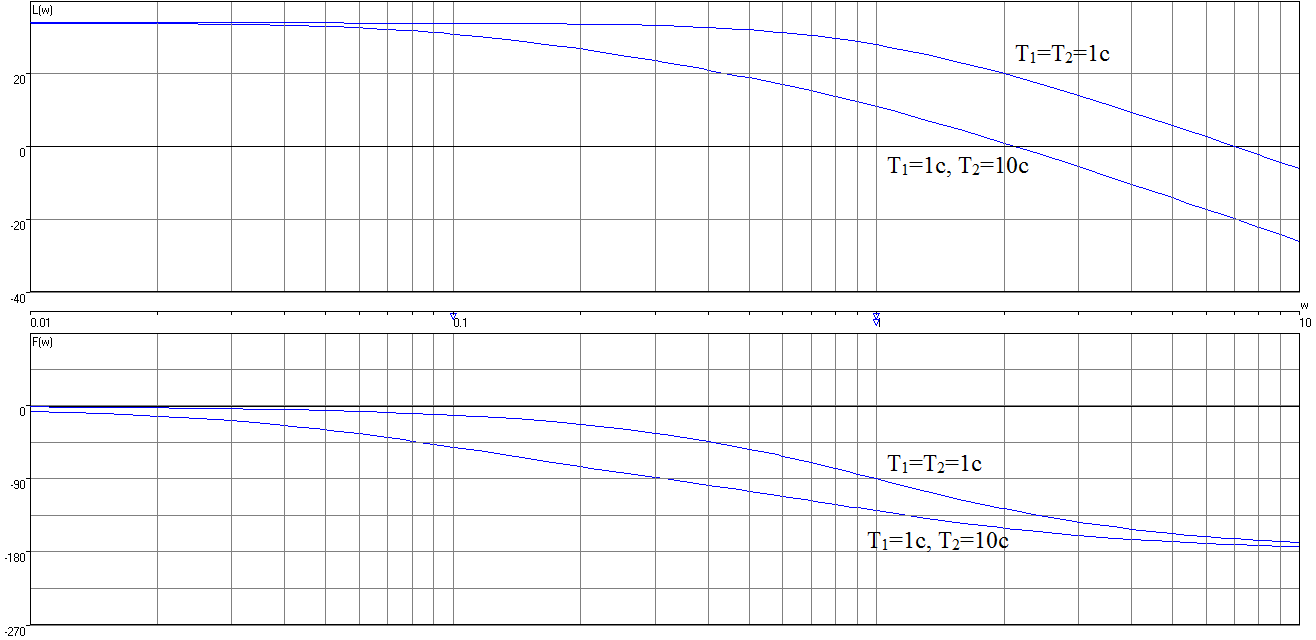
Рисунок 7 – ЛАЧХ и ЛФЧХ при варьировании параметра T2
Проанализируем корневую картину отдельных звеньев W1(s)=K1/(1+T1s), W2(s)=K2/(1+T2s) и всей системы управления с параметрами К1=5, К2=10, T1=1с, T2=10с.
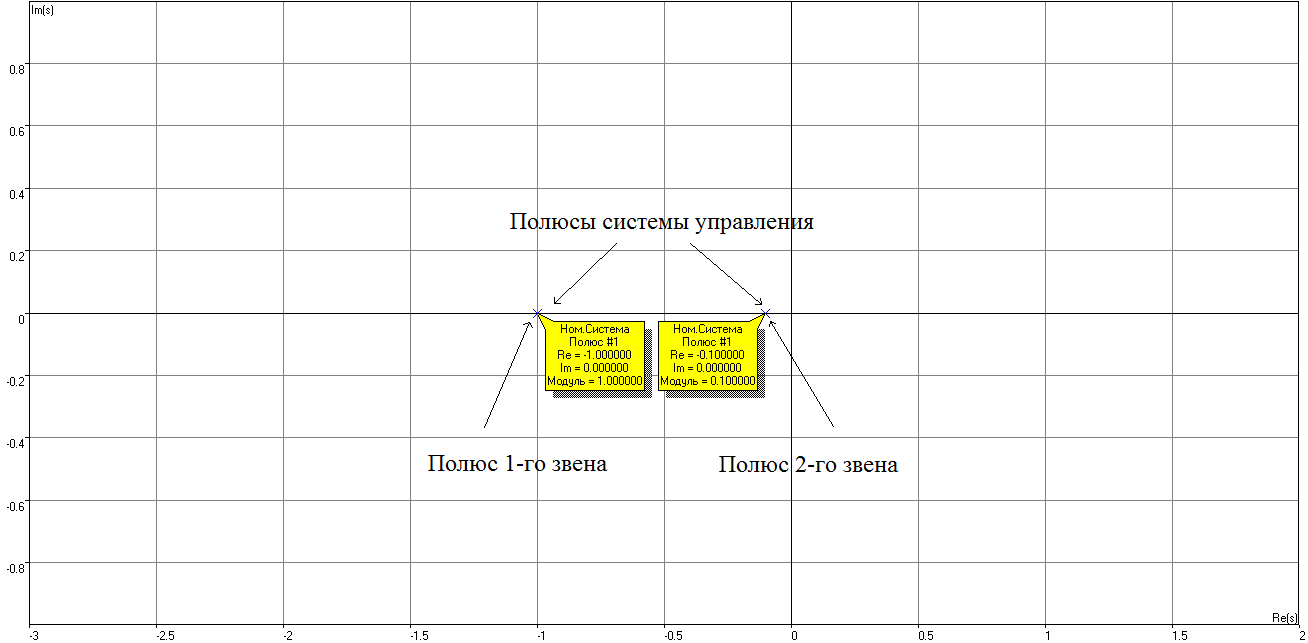
Рисунок 8 – Корневая плоскость отдельных звеньев и всей системы управления
1.3. Исследуем три звена, соединенных последовательно, с передаточными функциями W1(s)=K1/(1+T1s), W2(s)=K2/(1+T2s) и W3(s)= (1+T3s) при К1=5, K2=10. Порядок характеристического полинома – первый. Передаточная функция полученной системы будет иметь следующий вид:
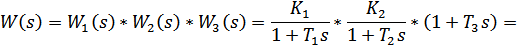
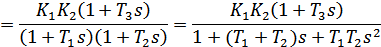
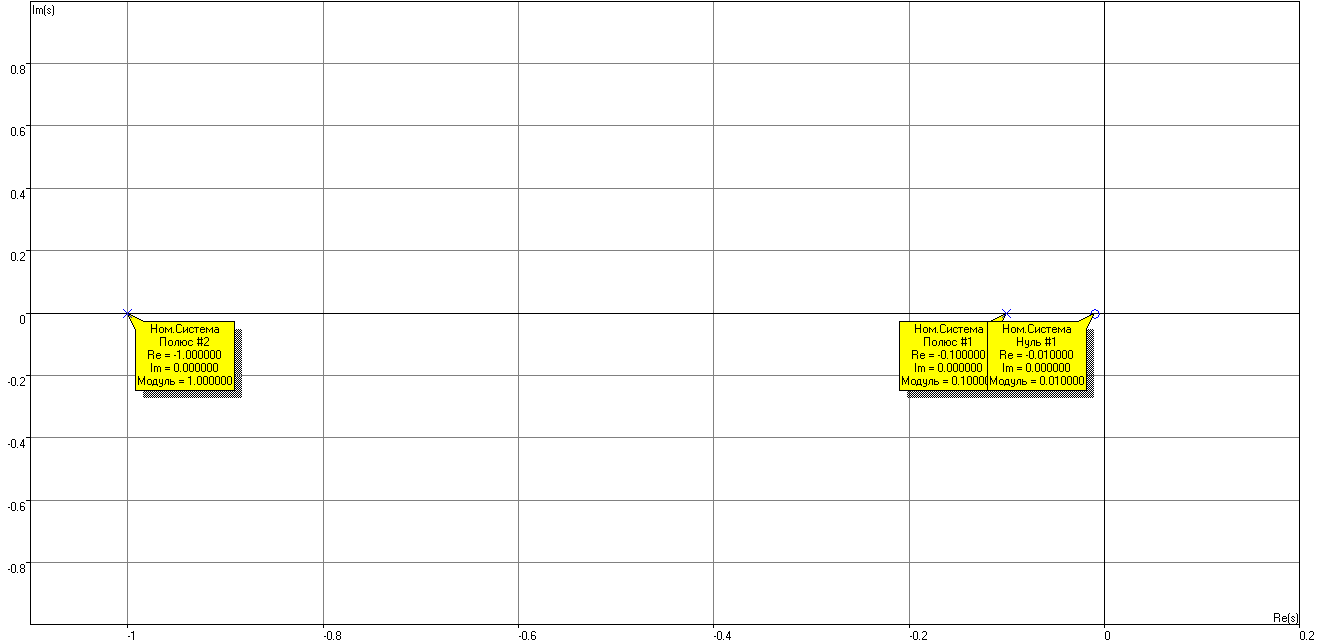
Рисунок 9 –Корневая плоскость при T1=1с, T2=10с, T3=100с
Нуль на рисунке 9 соответствует нулю звена с ПФ W3(s)= (1+T3s), полюса 1 и 2 – звеньям с ПФ W1(s)=K1/(1+T1s) и W2(s)=K2/(1+T2s) соответственно.

Рисунок 10 – Корневая плоскость при T1=1с, T2=T3=100с
При подстановке T1=1с, T2=T3=100с система будет иметь также 2 полюса и один нуль, причем нуль и первый полюс будут совпадать.
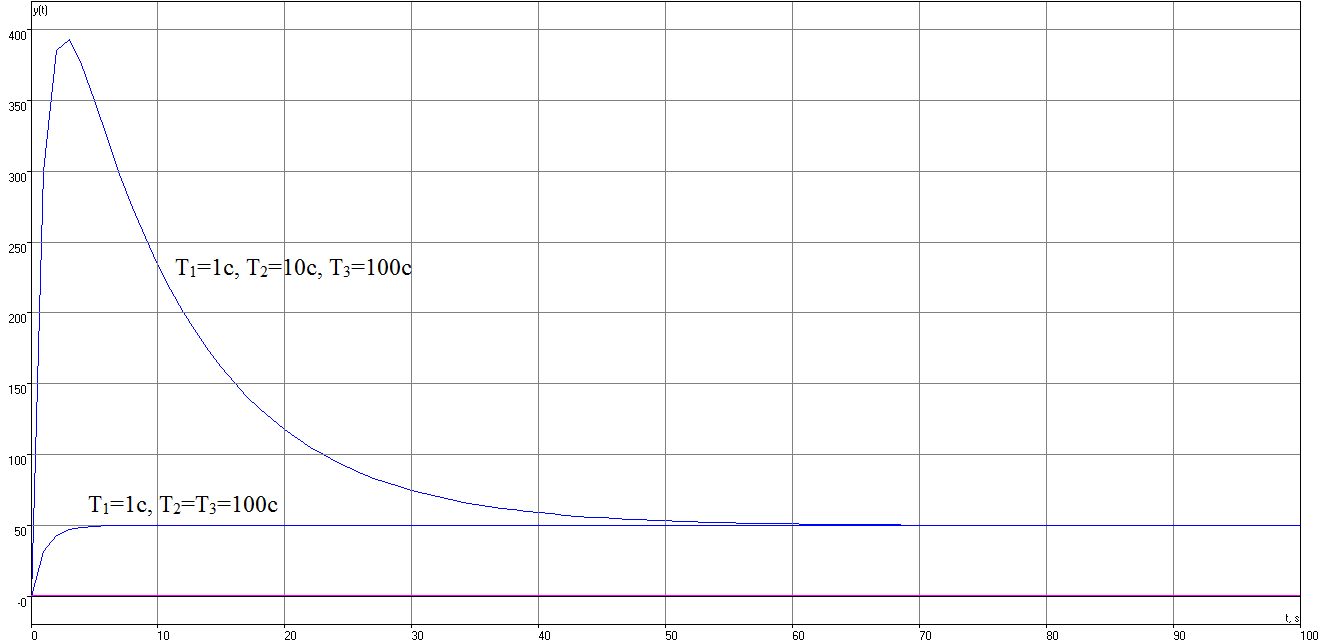
Рисунок 11 – Переходная характеристика при варьировании параметров T1, T2, T3
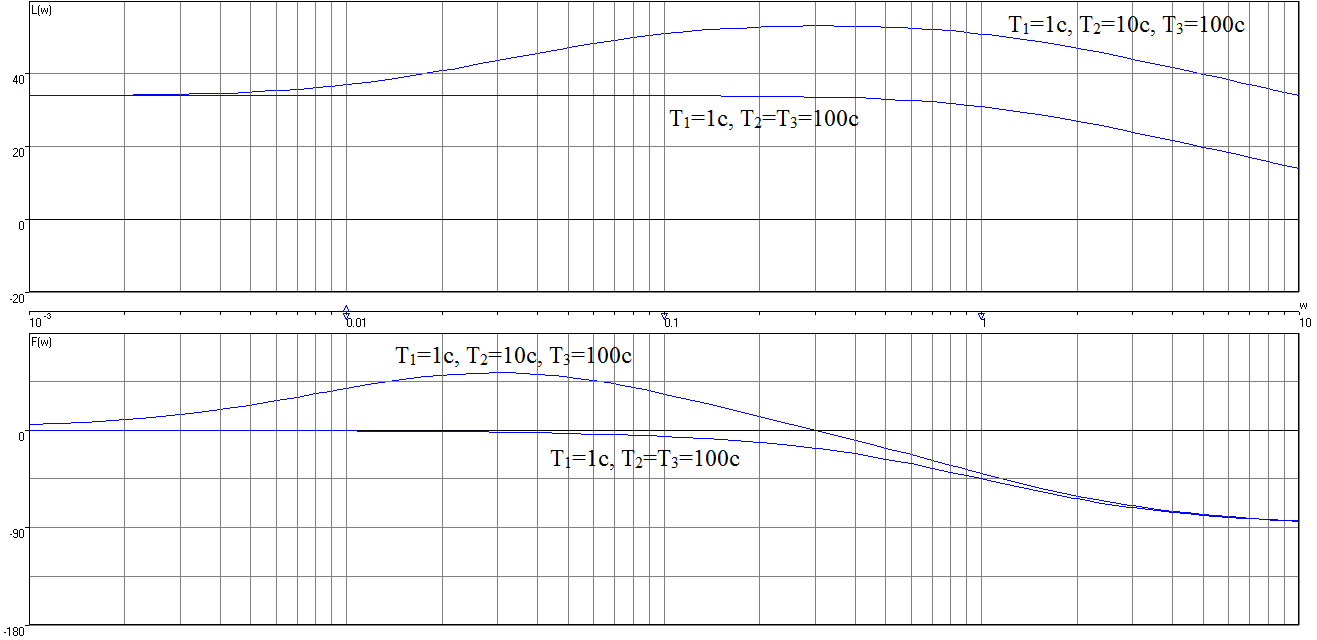
Рисунок 12 –ЛАЧХ и ЛФЧХ при вариации параметров T1, T2, T3
1.4. Исследуем два звена, соединенных последовательно, с передаточными функциями W1(s)=K(1+T1s) и W2(s)=1/(1-T2s) при К=5. Передаточная функция полученной системы будет иметь следующий вид:
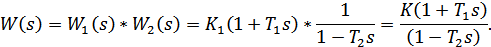
Исследуем систему при T1=T2=0,14с.
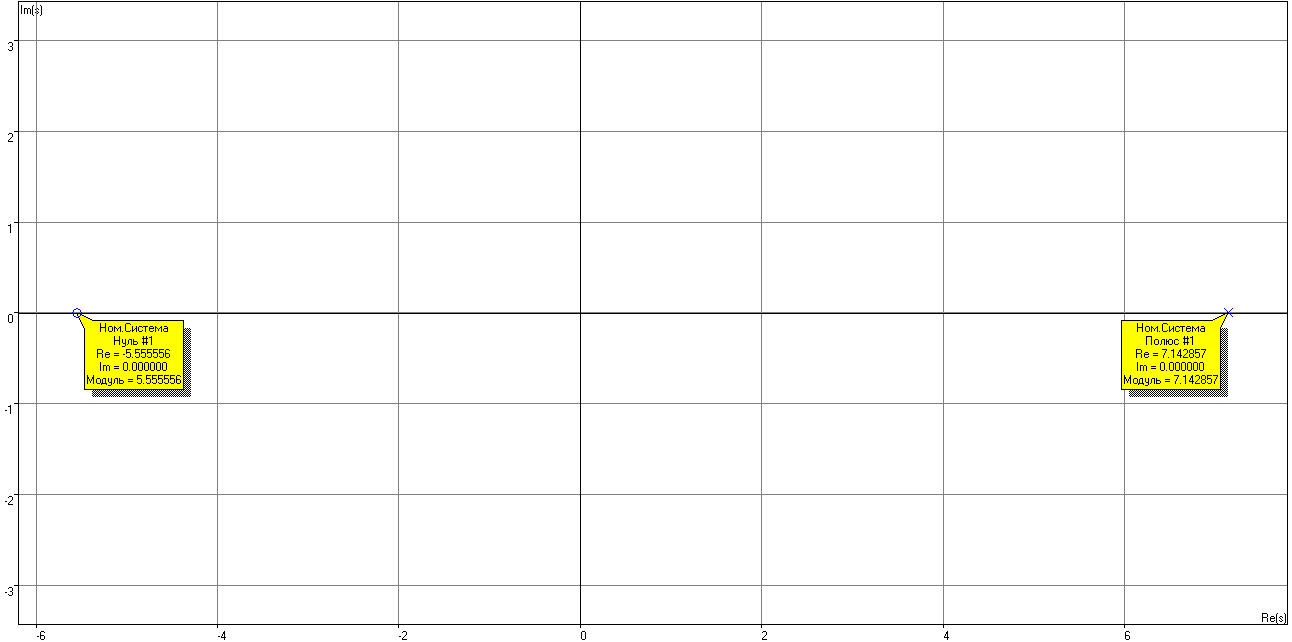
Рисунок 13 – Корневая плоскость

Рисунок 14 – Переходная характеристика
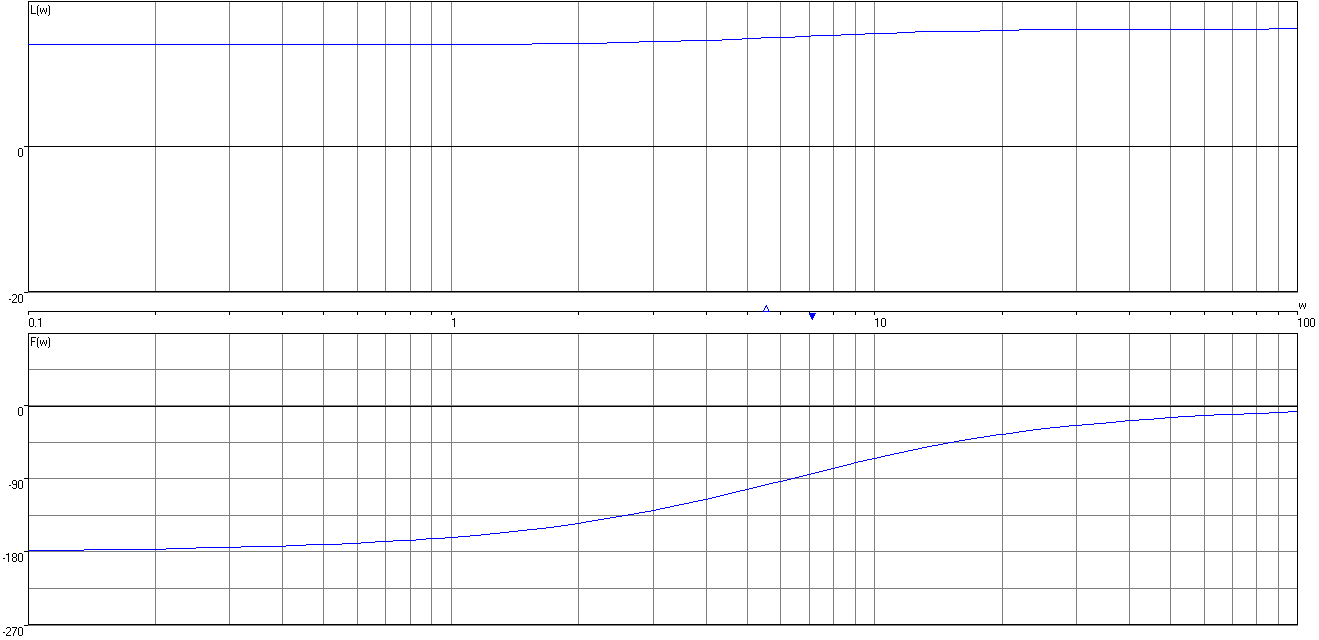
Рисунок 15 – ЛАЧХ и ЛФЧХ
Исследуем систему при T1=0,14с, T2=1,14с.
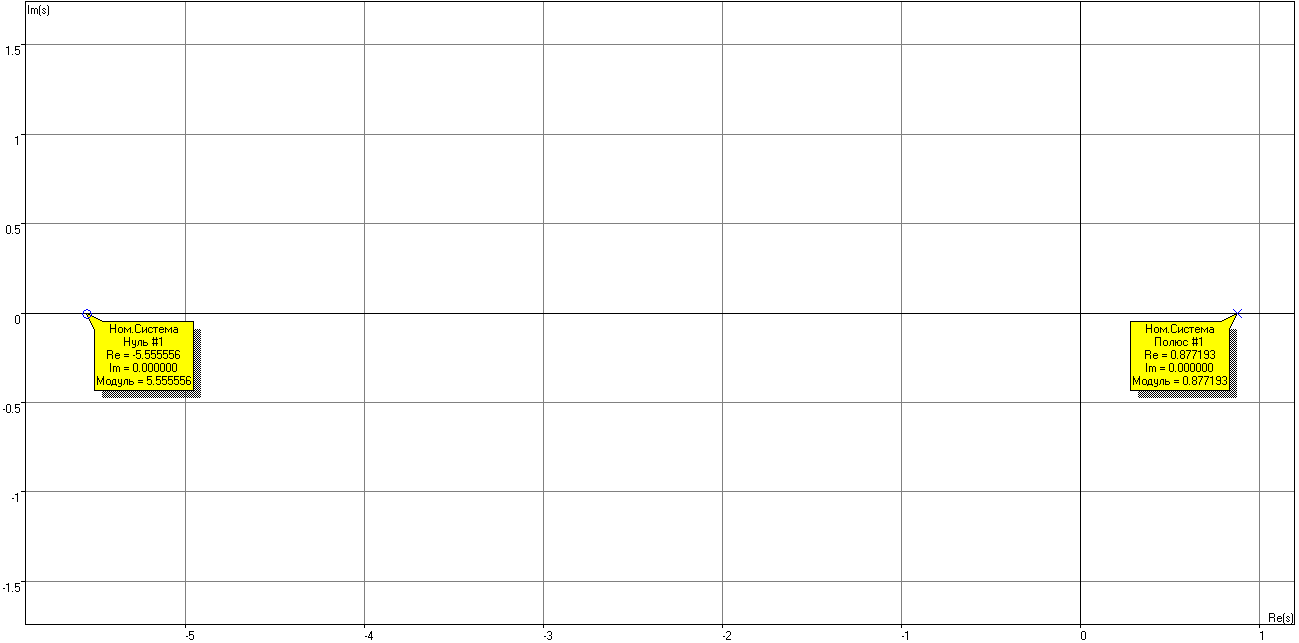
Рисунок 16 – Корневая плоскость
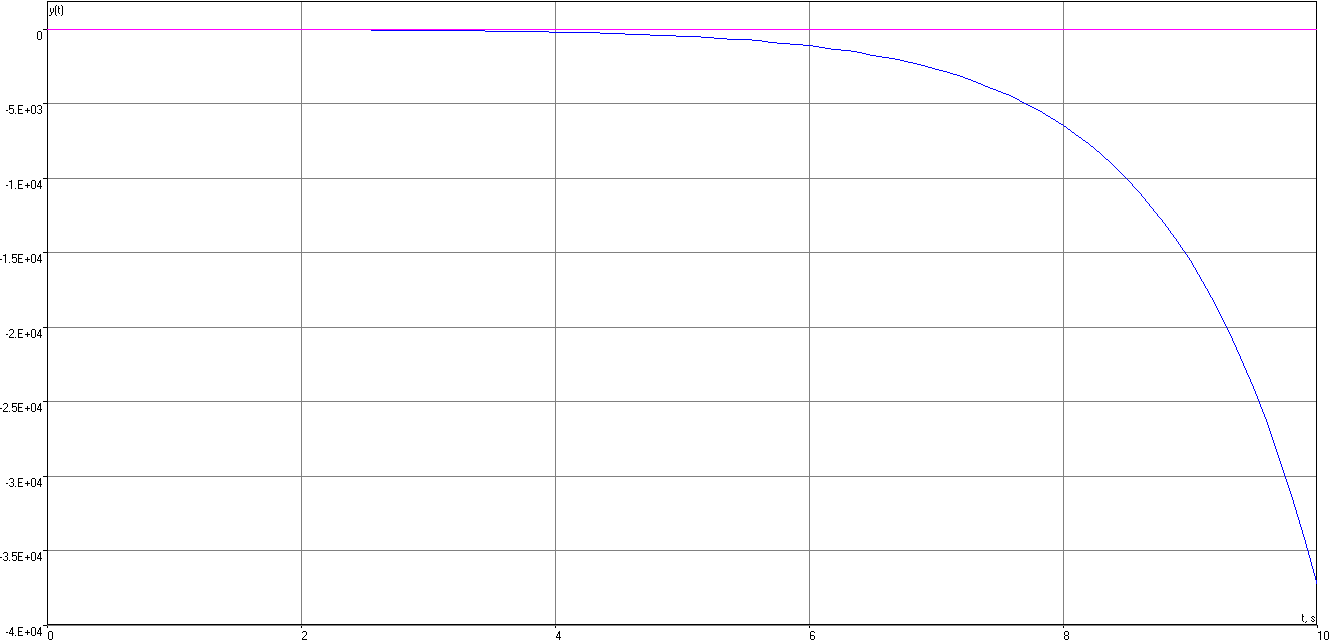
Рисунок 17 – Переходная характеристика
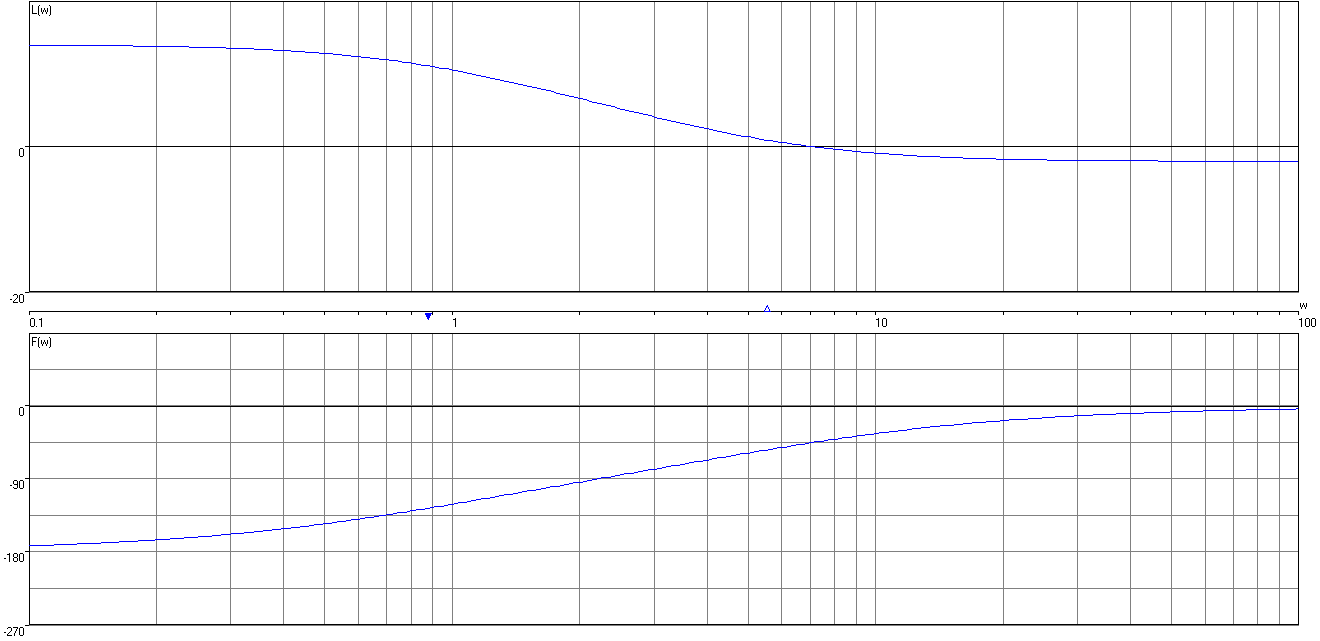
Рисунок 18 – ЛАЧХ и ЛФЧХ
При L(ω)=0 ω ср=7рад/с. При этом φ(ω)=–45,58о.
Таблица 1 – Сравнение с п.1.2
| Характеристика | 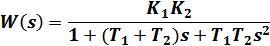 (пункт 1.2) (пункт 1.2) | 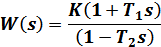 |
| Корневая плоскость | 2 полюса | 1 нуль и 1 полюс |
| Переходная характеристика | возрастающая | убывающая |
| ЛАЧХ | убывающая | убывающая |
| ЛФЧХ | убывающая от 0о до -180о | восходящая, [0о;-180о] |
 2015-05-10
2015-05-10 1081
1081