ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2
«Эконометрика»
Преподаватель ______________ В. А. Середа
Студент УБ11-02 431104391 ______________ А. В. Шибико
Красноярск 2013
| Субъекты РФ | Стиральные машины(Y) | Холодильники. Морозильники(X) |
| Белгородская область | ||
| Брянская область | ||
| Владимирская область | ||
| Воронежская область | ||
| Ивановская область | ||
| Калужская область | ||
| Костромская область | ||
| Курская область | ||
| Липецкая область | ||
| Московская область | ||
| Орловская область | ||
| Рязанская область | ||
| Смоленская область | ||
| Тамбовская область | ||
| Тверская область | ||
| Тульская область | ||
| Ярослваская область | ||
| Республика Карелия | ||
| Республика Коми | ||
| Архангельская область | ||
| Вологодская область | ||
| Калининградская область | ||
| Ленинградская область | ||
| Мурманская область | ||
| Новгородская область | ||
| Псковская область | ||
| Краснодарский край | ||
| Ставропольский край | ||
| Астраханская область | ||
| Волгоградская область | ||
| Ростовская область | ||
| Республика Башкортостан | ||
| Республика Марий Эл | ||
| Республика Мордовия | ||
| Республика Татарстан | ||
| Удмуртская Республика | ||
| Чувашская Республика | ||
| Кировская область | ||
| Нижегородская область | ||
| Оренбургская область | ||
| Пензенская область | ||
| Пермская область | ||
| Самарская область | ||
| Саратовская область | ||
| Ульяновская область |
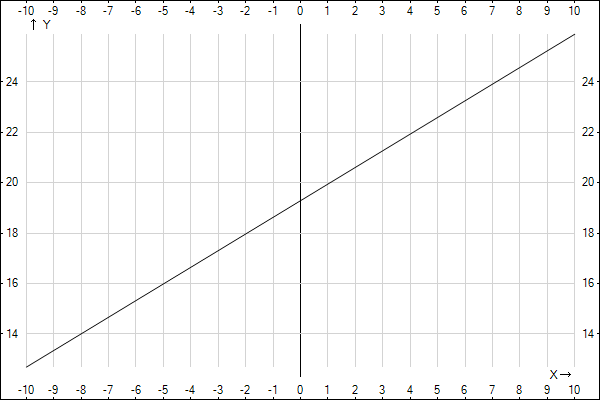
Построить предложенные уравнения регрессии, включая линейную регрессию.
1.1 Линейная регрессия описывается уравнением 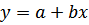 , коэффициенты которого находятся по соответствующим формулам:
, коэффициенты которого находятся по соответствующим формулам:
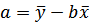
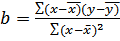
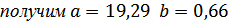
Линейное уравнение регрессии будет иметь вид 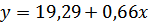
1.2 Параболическое уравнение регрессии имеет вид 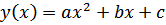 , коэффициенты которого можно найти, решив следующую систему:
, коэффициенты которого можно найти, решив следующую систему:
Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами:
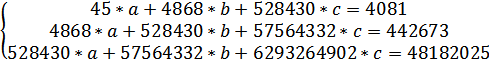
Решение системы:
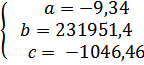
Параболическое уравнение регрессии:
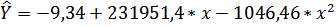
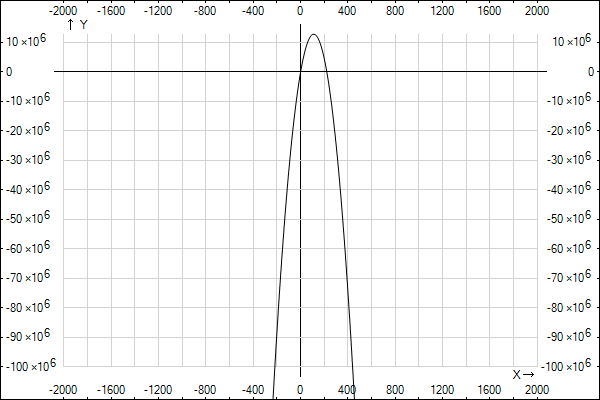
Вычислить индексы парной корреляции для каждого уравнения.
1.3 Для нахождения коэффициентов гиперболического уравнения регрессии, которое имеет вид  решим систему уравнений:
решим систему уравнений:

Система нормальных уравнений с вычисленными коэффициентами:
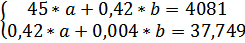
Решение системы:
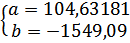
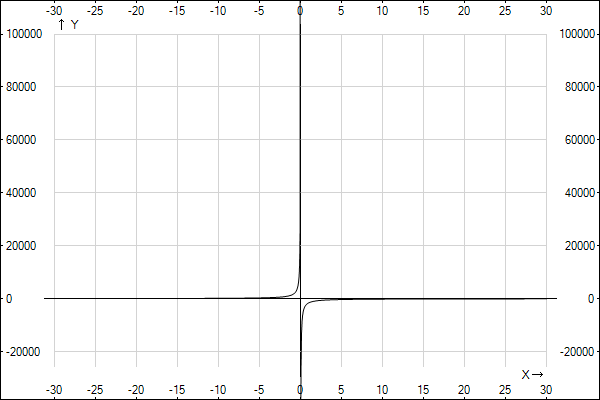
Гиперболическое уравнение регрессии:
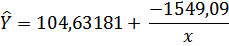
 2015-05-10
2015-05-10 631
631







