Поверка значимости уравнения регрессии и отдельных коэффициентов линейного уравнения

1) проверка значимости уравнения в целом

Пусть H0: уравнение статистически незначимо

H1: уравнение статистически значимо

Оценку статистической значимости уравнения регрессии в целом

проведем с помощью F -критерия Фишера. Фактическое значение F -

критерия по формуле составит

F_факт=

где ρ = 1

Тогда получим

F_факт = 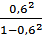× 43 = 24,1875

Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы k₁ =1 и k₂ =45 -2 =43 составляет

F _табл= 4,07. Так как F_факт =24,1875> F_табл = 4,07

Вывод: Выполняется условие 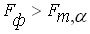, то ошибочное обнаружение связи со значением 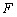-критерия равным или большим 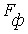по выборке из генеральной совокупности с несвязанными между собой переменными будет происходить с вероятностью меньшей чем уровень значимости. В соответствии с правилом “очень редких событий не бывает”, приходим к выводу, что установленная по выборке связь между переменными имеется и в генеральной совокупности, из которой она получена.

2) Проверка значимости отдельных коэффициентов линейного уравнения

Определим стандартные ошибки параметров линейной регрессии и коэффициента корреляции.

Остаточная дисперсия на одну степень свободы

S²_ост = 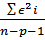, где 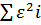= =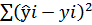1429,36

S²_ост = 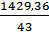= 33,24

ρ_а= 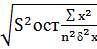= = 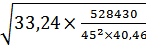14,64

Где 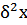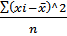_{= =}1820,58/45=40,46

ρ_b= 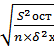= = 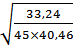0,14

S _ai = 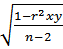= = 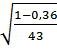0,12

Тогда

t_a= 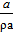= = 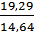1,32

t_b= 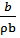= 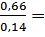4,71

Вывод: Практические значения t -статистики коэффициента b превосходит табличное значение, поэтому параметр статистически значим.