Метод перебора

Будем отыскивать минимум функции 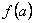на отрезке [a,b]. Допустим, что целевая функция унимодальна, т.е. на данном отрезке она имеет только один минимум. Отметим, что в инженерной практике обычно встречаются именно такие целевые функции. Погрешность приближенного решения задачи определяется разницей между оптимальным значением проектного параметра и принятым приближением к нему 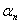. Потребуем, чтобы эта погрешность была по модулю меньше заданного допустимого значения .

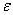Процесс решения задачи методом перебора состоит в последовательном сужении интервала изменения проектного параметра, называемого интервалом неопределенности. В начале процесса оптимизации его величина составляет b-a, а в конце процесса она должна стать меньше 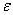, т.е. оптимальное значение проектного параметра должно находиться в интервале неопределенности 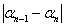, причем .

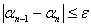В качестве приближения к оптимальному значению можно принять любое значение

,

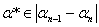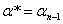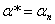например, или , или

.

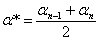Наиболее простым способом сужения интервала неопределенности является деление его на некоторое количество равных частей с дальнейшим вычислением целевой функции в точках разбиения. Сравнивая полученные значения 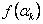, отыскиваем среди них наименьшее.

Пример:

Проиллюстрируем суть метода равномерного поиска посредством рассмотрения задачи нахождения минимума.

Пусть задана функция

.

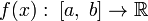И задача оптимизации выглядит так:

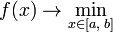
Пусть также задано число наблюдений .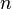

Тогда отрезок 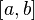разбивают на 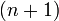равных частей точками деления:

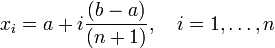
Вычислив значения 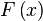в точках 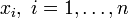, найдем путем сравнения точку 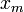, где 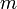— это число от 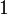до 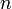такую, что

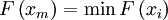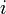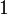для всех от до .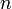

Тогда интервал неопределённости составляет величину 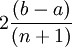, а погрешность определения точки минимума 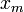функции 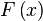соответственно составляет: .

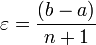Метод “золотого сечения”

Пусть задана функция 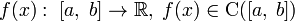. Тогда для того, чтобы найти определённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точк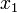и и 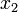такие, что:

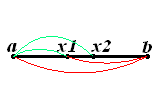
Рис. 2 Иллюстрация выбора промежуточных точек

метода золотого сечения

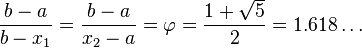, где 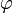— пропорция золотого сечения.

Таким образом:

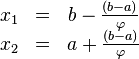
То есть точка 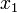делит отрезок 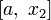в отношении золотого сечения. Аналогично 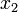делит отрезок 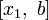в той же пропорции. Это свойство и используется для построения итеративного процесса.