Методы одномерной оптимизации

Разработал преподаватель-стажёр кафедры технологий программирования

Воронько Д.Е.

Полоцк, 2013

Краткая теория:

Одномерная задача оптимизации в общем случае формируется следующим образом. Найти наименьшее или наибольшее значение целевой функции 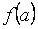, заданной на множестве 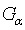, и определить значение проектного параметра 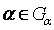, при котором целевая функция принимает экстремальное значение. Существование решения поставленной задачи определяется Вейерштрасса: любая функция 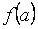, непрерывная на отрезке [a,b], принимает на этом отрезке наименьшее и наибольшее значения. На рис. 1 проиллюстрирован смысл сформулированной теоремы.

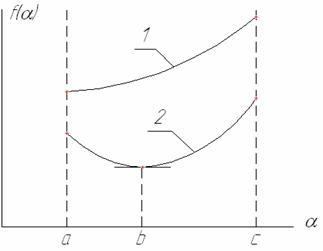
Рис. 1. К теореме Вейерштрасса.

Функция 1, не имеющая экстремума, достигает наименьшего значения при α=a и наибольшего значения при α=b. Функция 2, содержащая экстремум, достигает наименьшего значения в точке экстремума α=c и наибольшего при α=b.

Если функция 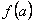задана аналитически, то она может достигать своего наибольшего и наименьшего значения либо в граничных точках отрезка [a,b], либо в экстремальных точках, в которых производная 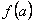обращается в нуль. Тогда для определения наибольшего или наименьшего значения функции 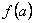на отрезке [a,b] необходимо вычислить ее значения во всех экстремальных и граничных точках и сравнить полученные значения. Наименьшее или наибольшее из них и будет искомым значением.

Иногда, когда целевая функция задана таблично или может быть вычислена при некоторых дискретных значениях аргумента, используются различные методы поиска.