Биномиальное распределение

Лабораторная работа № 4

Постройте биноминальное распределение для серии из n независимых испытаний с вероятностью успеха p, пуассоновское распределение с параметром λ, гипергеометрическое распределение с параметрами N, M, n, геометрическое распределение с параметрами n, p. Для каждого распределения выполните следующее:

1) проверьте равенство ;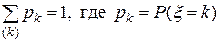

2) найдите значение k, для которого величина 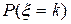максимальна (для биноминального распределения);

3) постройте графики распределения и функций распределения;

4) вычислите вероятность попадания значений случайной величины в интервал (a, b).

№	n	p	λ	N	М	а	b
		0.1	1.00
		0.11	0.95
		0.12	0.90
		0.13	0.85
		0.14	0.80
		0.15	0.75
		0.16	0.70
		0.17	0.65
		0.18	0.60
		0.19	0.55
		0.20	0.50
		0.21	1.05
		0.22	1.10
		0.23	1.15
		0.24	1.25
		0.25	1.30
		0.26	1.35
		0.27	1.40
		0.28	1.45
		0.29	1.50

Пример выполнения задания

Биномиальное распределение.

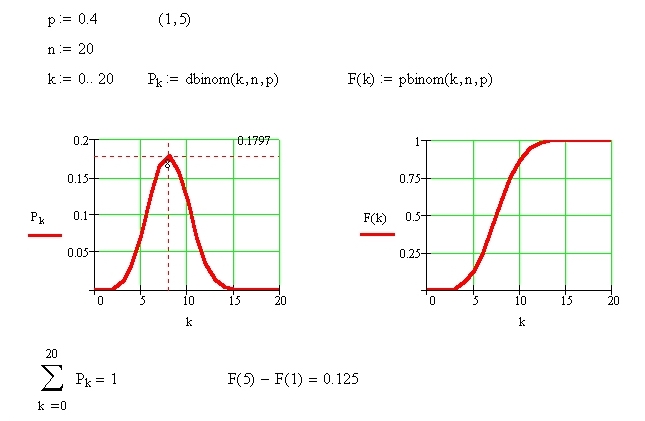
Для того, чтобы определить по графику распределения наиболее вероятное значение случайной величины, щелкните в меню Формат в пункте График по строке След, установите перекрестье маркера на точке максимума распределения и введите в рабочий документ вероятность значения, указанного в окне X-Value (Величина Х).Для исследуемой случайной величины наиболее вероятное значение равно 8, вероятность этого события равна 0.18.

1 2 3 4 5

Подборка статей по вашей теме: