Ранжированная переменная отличается от вектора (одномерного массива) тем, что невозможно использование ее отдельных значений. При необходимости иметь доступ к каждому значению переменной со многими компонентами она должна быть задана в виде одномерного (вектора) и двумерного (матрицы) массива.
Местоположение элемента массива задается одним индексом для вектора и двумя для матрицы. Индексы могут быть только положительными целыми числами. Для ввода индекса используется знак «[» – прямая открывающая скобка.
Для задания массивов можно либо воспользоваться командой Matrices меню Math, либо нажать комбинацию клавиш Ctrl+V, либо щелкнуть на значке с изображением шаблона матрицы. Любое из этих действий вызывает появление диалогового окна, в котором надо указать количество строк m и столбцов n в массиве. При m=1 получим вектор-столбец, а при n=1 – вектор-строку.
В отношении массивов действуют те же правила присваивания и вывода, что и для обычных переменных. В частности, с помощью оператора присваивания можно создать массив заданного размера и заданного типа без ручного заполнения шаблона (рисунок 2.2.).
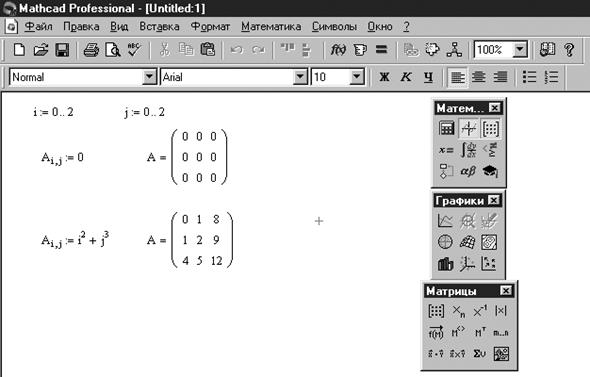
Рис. 2.2. Пример создания матриц без использования шаблонов матриц
Для работы с массивами Mathcad содержит ряд операторов и функций. Ниже представлены операторы для работы с векторами и матрицами. В таблице используются следующие обозначения: V – для векторов, M – для матриц, Z – для скалярных величин.
| Оператор | Ввод | Описание |
| V1+V2 | V1+V2 | Сложение векторов V1 и V2 |
| V1-V2 | V1-V2 | Вычитание векторов V1 и V2 |
| -V | -V | Смена знака у элементов вектора V |
| -M | -M | Смена знака у элементов матрицы M |
| V-Z | V-Z | Вычитание из всех элементов вектора V скаляра Z |
| Z*V, V*Z | Z*V, V*Z | Умножение вектора V на скаляр Z |
| Z*M, M*Z | Z*M, M*Z | Умножение матрицы M на скаляр Z |
| V1*V2 | V1*V2 | Скалярное умножение векторов V1 и V2 |
| M*V | M*V | Умножение матрицы M на вектор V |
| M1*M2 | M1*M2 | Умножение матрицы M1 на матрицу M2 |
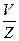
| V/Z | Деление всех элементов вектора V на скаляр Z |
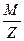
| M/Z | Деление всех элементов матрицы M на скаляр Z |
| M-1 | M^-1 | Обращение матрицы M |
| Mn | M^n | Возведение матрицы M в степень n |
| |V| | |V | Вычисление модуля вектора V |
| |M| | |M | Вычисление определителя матрицы M |
| VT | V Ctrl+! | Транспонирование вектора V |
| MT | M Ctrl+! | Транспонирование матрицы M |
| V1´V2 | V1 Ctrl+* V2 | Векторное умножение векторов V1 и V2 |
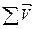
| Alt+$ V | Вычисление суммы элементов вектора V |
| M<n> | M Ctrl+^ n | Выделение n-ого столбца матрицы M |
| Vn | V[n | Выделение n-ого элемента вектора V |
| Mm,n | M[(m,n) | Выделение элемента (m, n) матрицы M |
Существует ряд встроенных векторных и матричных функций. Они облегчают решение задач линейной алгебры и других сфер приложения векторов и матриц.
| length(V) | возвращает число элементов вектора |
| last(V) | возвращает номер последнего элемента вектора |
| max(V) | возвращает максимальный по значению элемент вектора или матрицы |
| min(V) | возвращает минимальный по значению элемент вектора или матрицы |
| augment(M1,M2) | объединяет в одну две матрицы, имеющие одинаковое число строк (объединение идет бок о бок) |
| identity(n) | создает единичную квадратную матрицу размером n*n |
| stack(M1,M2) | объединяет в одну две матрицы, имеющие одинаковое число столбцов, располагая М1 над М2 |
| submatrix(A,ir,jr,ic,jc) | возвращает субматрицу, состоящую из всех элементов содержащихся в строках от ir по jr и столбцов с ic по jc (ir£jr и ic£jc) |
| diag(V) | создает диагональную матрицу, элементы главной диагонали которой равны элементам вектора V |
| matrix(m,n,f) | создает матрицу, в которой (i, j) элемент равен f(i,j), где i=0, 1, …, m и j=0, 1, …, n; f(i,j) - некоторая функция |
| cols(M) | возвращает число столбцов матрицы M |
| rows(M) | возвращает число строк матрицы M |
| rank(M) | возвращает ранг матрицы M |
| tr(M) | возвращает след (сумму диагональных элементов) матрицы M |
| mean(M) | возвращает среднее значение элементов матрицы M |
Примеры работы с матрицами приведены на рисунке 2.3.
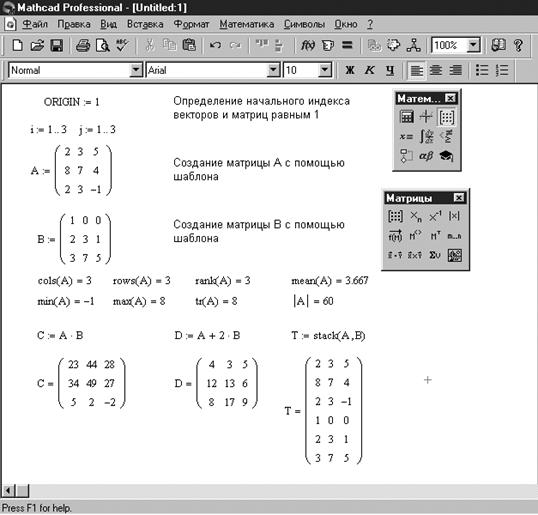
Рис. 2.3. Примеры работы с матрицами
 2015-05-10
2015-05-10 548
548








