Функция 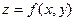 имеет максимум (минимум) в точке
имеет максимум (минимум) в точке 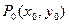 , если существует такая окрестность точки Р0 , для всех точек Р(х, у) которой, отличных от точки Р0, выполняется неравенство
, если существует такая окрестность точки Р0 , для всех точек Р(х, у) которой, отличных от точки Р0, выполняется неравенство 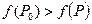 (соответственно
(соответственно 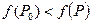 ). Точки минимума и максимума функции
). Точки минимума и максимума функции 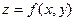 называются точками экстремума этой функции.
называются точками экстремума этой функции.
Необходимое условие экстремума. Если дифференцируемая функция 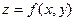 имеет экстремум в точке
имеет экстремум в точке 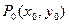 , то в этой точке
, то в этой точке 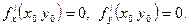
Т.е. если 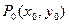 - точка экстремума функции
- точка экстремума функции 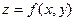 , то либо частные производные в этой точке равны нулю (в этом случае точку
, то либо частные производные в этой точке равны нулю (в этом случае точку 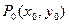 называют стационарной точкой), либо функция
называют стационарной точкой), либо функция 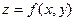 в этой точке не является дифференцируемой.
в этой точке не является дифференцируемой.
Достаточное условие экстремума. Пусть 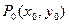 - стационарная точка функции
- стационарная точка функции 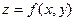 , причем эта функция дважды дифференцируема в некоторой окрестности точки Р0 и все ее вторые производные непрерывны в точке Р0. Вычислим
, причем эта функция дважды дифференцируема в некоторой окрестности точки Р0 и все ее вторые производные непрерывны в точке Р0. Вычислим
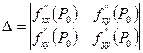 .
.
Тогда:
- если 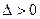 , то функция
, то функция 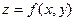 имеет в точке
имеет в точке 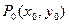 экстремум: максимум при
экстремум: максимум при 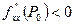 (или при
(или при 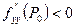 ), минимум при
), минимум при 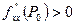 (или при
(или при 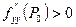 );
);
- если 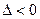 , то в точке
, то в точке 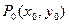 экстремума нет;
экстремума нет;
- если 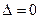 , то требуется дополнительное исследование.
, то требуется дополнительное исследование.
Пример 7. Исследуем на экстремум функцию 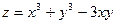 .
.
Решение. Найдем частные производные первого порядка:
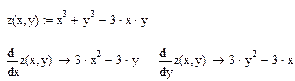
Решив систему уравнений
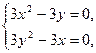
найдем две стационарные точки 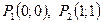 .
.
Найдем значения частных производных второго порядка и вычислим 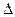 в точке
в точке 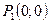 :
:
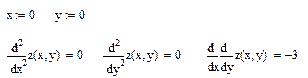
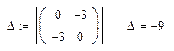
Т.к. в точке 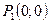
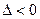 , то экстремума в этой точке нет.
, то экстремума в этой точке нет.
Найдем значения частных производных второго порядка и вычислим 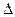 в точке
в точке 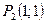 :
:
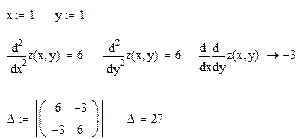
Т.к. в точке 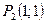
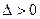 и
и 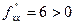 , то в точке
, то в точке 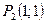 функция имеет минимум, равный
функция имеет минимум, равный
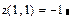
 2015-05-10
2015-05-10 318
318








