Кроме экстремума в точке, для функции двух переменных рассматривается условный экстремум, т. е. экстремум функции 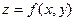 , найденный в предположении, что переменные х и у связаны соотношением
, найденный в предположении, что переменные х и у связаны соотношением 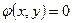 , которое называется уравнением связи.
, которое называется уравнением связи.
Задача нахождения условного экстремума сводится к исследованию на экстремум функции Лагранжа 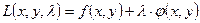 .
.
Необходимое условие условного экстремума выражается системой:
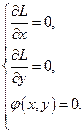
Пусть 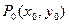 ,
, 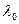 - некоторое решение этой системы.
- некоторое решение этой системы.
Достаточное условие условного экстремума. Вычислим определитель
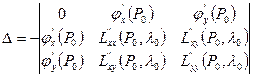 .
.
Если 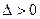 , то функция
, то функция 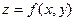 имеет в точке
имеет в точке 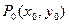 условный минимум; если
условный минимум; если 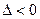 , то функция
, то функция 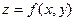 имеет в точке
имеет в точке 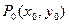 условный максимум.
условный максимум.
Пример 8. Найдем условный экстремум функции 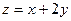 при условии
при условии 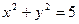 .
.
Решение. Составим функцию Лагранжа и найдем частные производные первого порядка:
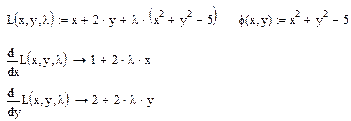
Система уравнений
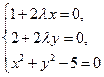
имеет два решения: 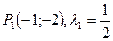 и
и 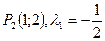 .
.
Вычислим 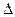 для каждого решения.
для каждого решения.
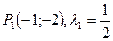 .
.
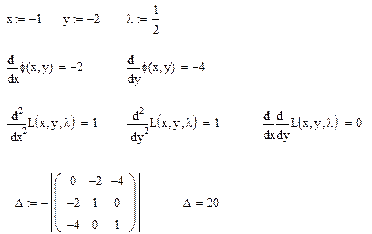
Т.к. 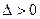 , то в точке
, то в точке 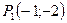 функция имеет условный минимум, равный
функция имеет условный минимум, равный 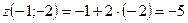 .
.
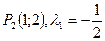 .
.
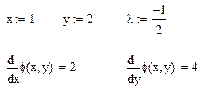
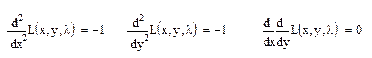
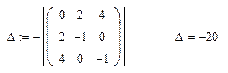
Т.к. 
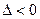 , то в точке
, то в точке 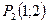 функция имеет условный минимум, равный
функция имеет условный минимум, равный 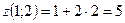 .
.
 2015-05-10
2015-05-10 308
308








