Задача корреляционно-спектрального анализа случайных сигналов состоит в получении оценок корреляционной функции 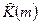
 и спектральной плотности мощности
и спектральной плотности мощности 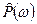 стационарной случайной последовательности
стационарной случайной последовательности 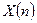 на основе обработки единственной реализации этого процесса конечной длительности N:
на основе обработки единственной реализации этого процесса конечной длительности N: 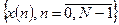 .
.
Отметим, что, если бы в нашем распоряжении было несколько реализаций 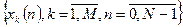 (ансамбль реализаций), то мы могли бы использовать формулу (8) для получения оценки
(ансамбль реализаций), то мы могли бы использовать формулу (8) для получения оценки 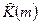 , заменив операцию математического ожидания усреднением по ансамблю реализаций
, заменив операцию математического ожидания усреднением по ансамблю реализаций
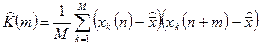 , где
, где 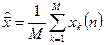 (11)
(11)
После этого мы бы применили (9) для получения оценки СПМ 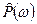 , подставив вместо
, подставив вместо 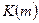 ее оценку
ее оценку 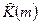 . Но, увы, в нашем распоряжении только одна реализация.
. Но, увы, в нашем распоряжении только одна реализация.
Выход из этого положения возможен, если исследуемая стационарная последовательность относится к классу т.н. эргодических последовательностей. В этом случае возможно замена операции усреднения по ансамблю реализаций усреднением по времени одной достаточно длинной реализации. В результате оценка корреляционной функции может быть рассчитана по следующей формуле:
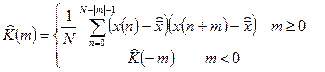 (11’)
(11’)
где оценка среднего 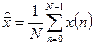 .
.
Общая длина оценки корреляционной функции 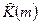 -
- 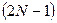 отсчетов:
отсчетов: 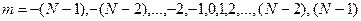 .
.
В качестве оценки СПМ 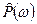 с учетом теоремы Винера-Хинчина логично взять следующую функцию:
с учетом теоремы Винера-Хинчина логично взять следующую функцию:
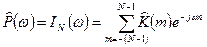 (12)
(12)
Функция 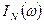 называется периодограммой. Впервые периодограмма, как средства анализа частотных свойств сигнала, была введена английским математиком А.Шустером в 1898 году в следующем виде.
называется периодограммой. Впервые периодограмма, как средства анализа частотных свойств сигнала, была введена английским математиком А.Шустером в 1898 году в следующем виде.
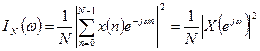 (13)
(13)
где  - Фурье-преобразование сигнала
- Фурье-преобразование сигнала 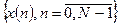 . Позднее было показано, что соотношения (12), (13) полностью эквивалентны.
. Позднее было показано, что соотношения (12), (13) полностью эквивалентны.
Отметим, что периодограммная оценка СПМ 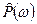 (12-13), как и всякая другая оценка, является случайной функцией частоты, т.е. для каждой новой реализации стационарной случайной последовательности
(12-13), как и всякая другая оценка, является случайной функцией частоты, т.е. для каждой новой реализации стационарной случайной последовательности 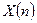 -
- 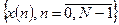 она ведет себя несколько по иному. Вероятностные свойства периодограммной оценки были исследованы и, в частности, установлены следующие два важных свойства. Математическое ожидание этой оценки равно свертке истинной СПМ
она ведет себя несколько по иному. Вероятностные свойства периодограммной оценки были исследованы и, в частности, установлены следующие два важных свойства. Математическое ожидание этой оценки равно свертке истинной СПМ 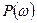 с функцией окна
с функцией окна 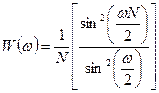 . При
. При 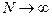 оценка становится несмещенной, но при конечных N смещение
оценка становится несмещенной, но при конечных N смещение 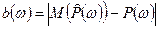 всегда присутствует: оно достаточно велико в местах быстрого изменения
всегда присутствует: оно достаточно велико в местах быстрого изменения 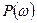 и мало на частотах, где
и мало на частотах, где 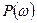 изменяется плавно. Можно представить ситуацию, когда при анализе суперпозиции двух синусоид с близкими частотами
изменяется плавно. Можно представить ситуацию, когда при анализе суперпозиции двух синусоид с близкими частотами 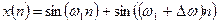 вследствие упомянутого свойства сглаживания периодограммная оценка принципиально не позволит обнаружить обе частотные компоненты. В связи с этим говорят о проблеме частотного разрешения спектральных оценок
вследствие упомянутого свойства сглаживания периодограммная оценка принципиально не позволит обнаружить обе частотные компоненты. В связи с этим говорят о проблеме частотного разрешения спектральных оценок 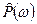 при конечных выборках. Частотное разрешение определяют путем задания минимальной разности частот
при конечных выборках. Частотное разрешение определяют путем задания минимальной разности частот 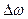 , такой, что математическое ожидание спектральной оценки
, такой, что математическое ожидание спектральной оценки 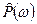 , полученной при анализе тестового сигнала
, полученной при анализе тестового сигнала 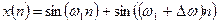 , позволит обнаружить обе частотные компоненты. Чем меньше
, позволит обнаружить обе частотные компоненты. Чем меньше 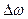 , тем лучше частотное разрешение. Для периодограммных оценок частотное разрешение
, тем лучше частотное разрешение. Для периодограммных оценок частотное разрешение 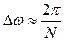 , т.е. улучшается с ростом длины выборочной реализации - N.
, т.е. улучшается с ростом длины выборочной реализации - N.
Но проблема смещенности не единственная для периодограммных спектральных оценок. Более существенной проблемой является то, что оценка 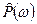 для всякой частоты
для всякой частоты 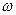 имеет очень большую дисперсию
имеет очень большую дисперсию 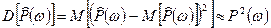 (иными словами, среднеквадратическое отклонение оценки равняется самому оцениваемому значению СПМ), которая не уменьшается с ростом N. В результате оценка СПМ (12) в целом не является состоятельной, поскольку ее среднеквадратическая ошибка, складывающаяся из квадрата смещения
(иными словами, среднеквадратическое отклонение оценки равняется самому оцениваемому значению СПМ), которая не уменьшается с ростом N. В результате оценка СПМ (12) в целом не является состоятельной, поскольку ее среднеквадратическая ошибка, складывающаяся из квадрата смещения 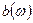 и дисперсии
и дисперсии 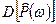
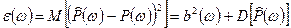 (15)
(15)
с ростом N не стремится к нулю.
Еще один важный теоретический результат состоит в том, что значения периодограммы, разнесенные по частоте на величину 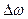 , кратную
, кратную  , являются некоррелированными. Это согласуется с ранее упомянутым частотным разрешением периодограммной оценки. В связи с этими обстоятельствами периодограммную оценку
, являются некоррелированными. Это согласуется с ранее упомянутым частотным разрешением периодограммной оценки. В связи с этими обстоятельствами периодограммную оценку 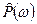 (12,13) от реализации длины N рекомендуется рассчитывать для N частот, кратных
(12,13) от реализации длины N рекомендуется рассчитывать для N частот, кратных  :
:
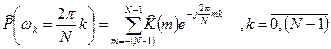 (16)
(16)
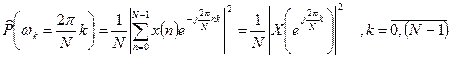 (17)
(17)
Учитывая симметрию 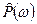 для анализа частотных свойств случайной последовательности достаточно рассматривать только половину частотных отсчетов периодограммной оценки (16,17)), вернее, чуть больше половины: k=0,1,2,,,, (N/2), всего (N/2+1) отсчетов. Отметим, что выражения (16), (17) могут быть эффективно рассчитаны с применением процедуры ДПФ-БПФ, далее мы рассмотрим эту возможность подробнее.
для анализа частотных свойств случайной последовательности достаточно рассматривать только половину частотных отсчетов периодограммной оценки (16,17)), вернее, чуть больше половины: k=0,1,2,,,, (N/2), всего (N/2+1) отсчетов. Отметим, что выражения (16), (17) могут быть эффективно рассчитаны с применением процедуры ДПФ-БПФ, далее мы рассмотрим эту возможность подробнее.
Резюмируем текущие результаты. Пусть в нашем распоряжении имеется одна реализация стационарной случайной последовательности процесса длительности N: 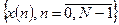 , и нам необходимо найти оценки
, и нам необходимо найти оценки
1) корреляционной функции 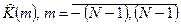 ;
;
2) спектральной плотности мощности 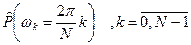 .
.
Очевидно, есть два возможных подхода к проведению корреляционно-спектрального анализа, определяемых порядком расчета оценок 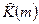 и
и 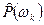 .
.
Первый подход. Сначала рассчитываем оценку корреляционной функции согласно (11’) 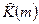 . Затем строим оценку СПМ с помощью формулы (16).
. Затем строим оценку СПМ с помощью формулы (16).
Второй подход. Сначала рассчитываем оценку СПМ согласно (17) с использованием процедуры БПФ. Здесь есть тонкий момент, если нам не нужна будет корреляционная функция, то достаточно будет СПМ рассчитать в N точках 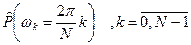 . Если N не является степенью двойки, то надо дополнить исходную реализацию до ближайшей степени двойки. Дополнять нужно либо средним значением по информативной части реализации, либо нулями – желательно обеспечить возможность выбора нужного варианта дополнения. Если нужна будет оценка корреляционной функции, то СПМ нужно рассчитать в два раза более густой сетке отсчетов:
. Если N не является степенью двойки, то надо дополнить исходную реализацию до ближайшей степени двойки. Дополнять нужно либо средним значением по информативной части реализации, либо нулями – желательно обеспечить возможность выбора нужного варианта дополнения. Если нужна будет оценка корреляционной функции, то СПМ нужно рассчитать в два раза более густой сетке отсчетов: 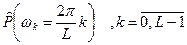 , где L=2N. Чтобы использовать БПФ, исходную реализацию нужно дополнить средним значением (не нулевым!!!) до степени двойки, ближайшей к (L=2N). (Пример: было N=100, стало L=256). После расчета оценки СПМ рассчитываем оценку корреляционной функции с помощью процедуры ОДПФ:
, где L=2N. Чтобы использовать БПФ, исходную реализацию нужно дополнить средним значением (не нулевым!!!) до степени двойки, ближайшей к (L=2N). (Пример: было N=100, стало L=256). После расчета оценки СПМ рассчитываем оценку корреляционной функции с помощью процедуры ОДПФ:
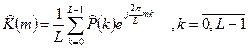 (18)
(18)
В силу специфики процедуры ДПФ-ОДПФ оценка 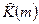 (18) определена при положительных значениях индекса m. Ее первые N отсчетов (
(18) определена при положительных значениях индекса m. Ее первые N отсчетов (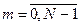 ) совпадают c неотрицательной половиной оценки (11’). Значений корреляционной оценки
) совпадают c неотрицательной половиной оценки (11’). Значений корреляционной оценки 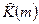 (18), соответствующие отрицательным сдвигам (m<0), находятся во второй половине рассчитанного массива
(18), соответствующие отрицательным сдвигам (m<0), находятся во второй половине рассчитанного массива 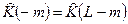 .
.
Отметим, что все современные программные пакеты анализа данных (MATLAB и другие) реализуют второй подход.
 2015-05-10
2015-05-10 1676
1676
