2015-05-10
1042
Взаимная корреляционная функция
Пусть даны выборочные реализации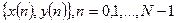 
двух случайных процессов с дискретным временем (случайных последовательностей) 
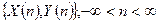. Если процессы являются стационарными и стационарно-связанными, то их важной количественной характеристикой является взаимная корреляционная функция
, 
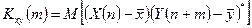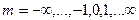(26)
Здесь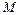 
- знак математического ожидания,
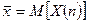- среднее значение первого процесса (отметим, что оно постоянно в случае стационарно-связанных процессов при всех 
),
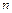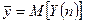- среднее значение второго процесса,
* - знак комплексного сопряжения (для действительнозначных процессов на него просто можно не обращать внимания).
Оценка этой важной характеристики по имеющимся конечным выборкам может быть вычислена в виде:
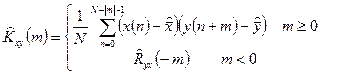(27)
где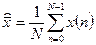 
, 
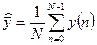- оценки средних значений по выборкам.
Обратите внимание, что общая длина корреляционной функции –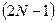 
- отсчетов, т.е. в два раза больше длин исходных реализаций.
Примечание 1: Как быть, если длины реализаций разные, например,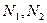 
.
Можно дополнить короткую реализацию своими средними значениями до большей длины и применить (27). При этом слева или справа несколько отсчетов оценки корреляционной функции будут нулевыми. Ну и пусть будут. А можно ничего не дополнять, а просто аккуратно реализовать вычисления в (1), подставляя в верхнем пределе суммы в случае расчета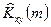 
вместо 
- 
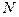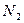, а при расчете 
- 
.
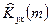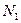При больших N целесообразно использовать более быстрый способ вычисления оценки корреляционной функции (27) на основе процедуры быстрого преобразования Фурье (БПФ). При этом обычно возрастают требования к размеру оперативной памяти.
Шаг 1. Центрируем исходные реализации (вычитаем из каждой свое среднее значение)
Шаг 2. Дополняем центрированные реализации нулями до ближайшей к удвоенной длине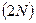 
степени двойки, например было 
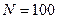, а стало 
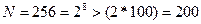. Это требование метода расчета процедуры БПФ по основанию 2.
Шаг 3. Находим с помощью БПФ дискретные преобразования Фурье (ДПФ) обеих расширенных последовательносте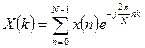й:
и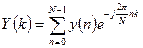 
, 
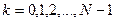
!!! Используем именно БПФ, иначе ничего не выиграем, а только проиграем.
Шаг 4. Составляем новый комплексный массив:
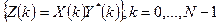
Шаг 5. Выполняем обратное преобразование Фурье c помощью БПФ
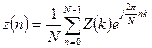
Шаг 6. Получаем оценку взаимной корреляционной функции:
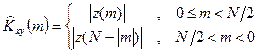(28)
Взаимная спектральная плотность мощности
Взаимная спектральная плотность мощности двух стационарно-связанных случайных процессов определяется как Фурье преобразование от взаимной корреляционной функции:
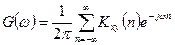(29)
Для ее оценивания используют два подхода:
а) корреляционный, когда предварительно строят оценку (27), а потом с помощью обратного БПФ получают оценку спектральной плотности
б) периодограммный, который применяется чаще и на котором мы остановимся.
Шаг 1. Расширяем исходные реализации вправо дополнением их среднего значения до ближайшей степени двойки. Т.е. было 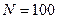, а стало 
.
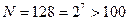Шаг 2. Находим с помощью БПФ дискретные преобразования Фурье (ДПФ) обеих расширенных последовательносте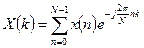й:
и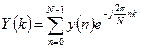 
, 
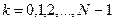
Шаг 3. Формируем «несглаженную» оценку взаимной спектральной плотности
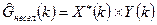
Шаг 4. Формируем сглаженную оценку
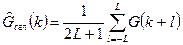(30)
На краях суммирование производится в предположении периодического продолжения области определения оценки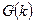 
по индексу k – [0,N-1].
Шаг 5. Отображение.
Замечание 1. В силу свойств симметрии оценки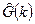 
достаточно отображать лишь первую половину отсчетов (
).
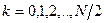Замечание 2. Оценка 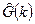- комплекснозначная, для отображения же нужны некие действительные функции. В системах обработки сигналов при проведении взаимного спектрального анализа обычно предоставляется возможность отображения следующих шести действительнозначных функций:
1. 
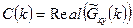- т.н. “синфазная” составляющая спектра (реальная часть)
2. 
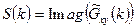- “квадратурная” составляющая спектра (мнимая часть)
3. 
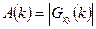- модуль взаимного спектра
4. 
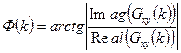- фаза взаимного спектра
5. 
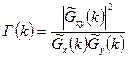- оценка функции когерентности
6. 
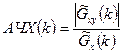- оценка амплитудно-частотной характеристики фильтра, преобразующего процесс X(n) в Y(n).
Примечание: в последних двух случаях нужны сглаженные периодограммные оценки спектральных плотностей исходных процессов:
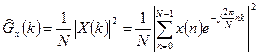
а затем проводится сглаживание с тем же параметром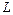 
(см. выше).
