Специальные классы функций спроса в моделях потребления

Как отмечено выше, между целевой функцией потребителя и функцией спроса существует взаимная связь. Если в модели потребительского выбора цены на блага и располагаемый бюджет потребителя являются независимыми факторами, то решением оптимизационной задачи является вектор – функция 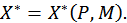Она может быть получена аналитически, либо путем статистического обобщения оптимальных решений для различных значений и . Компонентами вектор - функции являются функции 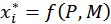спроса на товар .

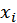Функции спроса характеризуют зависимости, которые легко обнаруживаются и проверяются эмпирически (в отличие от целевой функции потребителей). По этой причине функции спроса, подтверждаемые статистическими данными, представляют возможность определения целевой функции потребителя и (или) ее параметров.

Среди функций спроса наибольшее распространение получили однофакторные функции, отражающие зависимость спроса от уровня дохода домашних хозяйств. Соответствующие этим функциям кривые называются кривыми Э. Энгеля[6]. В обобщенной форме эти кривые можно выразить формулой 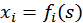, где s – средний доход, 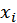– объем потребления i - го блага (либо объем спроса в случае, если он удовлетворяется).

Формы кривых могут быть различными. Например, если в определенной группе потребителей спрос на данный товар возрастает примерно в той же пропорции, что и доход, то зависимость будет линейной[7]. Если с ростом дохода спрос на определенную группу товаров растет более высокими темпами, то соответствующая кривая - выпукла (вниз). Если рост спроса с определенного момента отстает от роста дохода, то кривая - вогнута (вверх).

Насыщение спроса – категория, отражающая характерное для многих товаров и услуг существенное сокращение или прекращение спроса при увеличении дохода (снижении цен)[8]. Достигнутый уровень потребления – предельный.

Графически насыщение спроса изображается вогнутой кривой, имеющей тенденцию к росту, который замедляется, стремясь к предельному значению, называемому точкой насыщения.

Тот же принцип разграничения товаров по типу функций спроса от дохода использовал Л. Торнквист, предложивший специальные виды функции спроса (функции Торнквиста) для трех групп товаров: первой необходимости, второй необходимости и предметов роскоши. Кривые, соответствующие этим функциям, отличаются уровнями насыщения (для товаров первой необходимости) и уровнями доходов, инициирующих приобретение товаров второй необходимости и предметов роскоши.

Функция Торнквиста для товара первой необходимости имеет следующий вид:

где 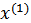- уровень потребления блага 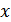, соответствующий уровню 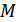потребительского дохода. Параметры 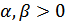зависят от цены блага, предполагаемой фиксированной.

Зависимость (2.61) отражает тот факт, что рост спроса на первоочередные товары с ростом дохода замедляется 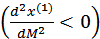и имеет предел 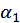(кривая спроса асимптотически приближается к прямой 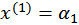, рис. 2.11).

По Торнквисту функция спроса на товары второй необходимости («относительной роскоши») имеет следующий вид:

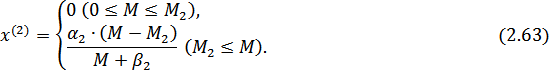
Эта зависимость также имеет предел 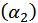, но более высокого уровня; при этом спрос на эту группу товаров появляется лишь после того, как доход достигнет величины .

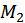Графиком рассматриваемой функции является кривая II на рис. 2.11.

Функция Торнквиста для предметов роскоши имеет вид:

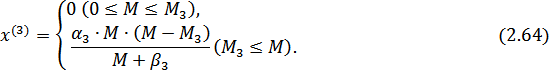
Эта функция не ограничена. Спрос возникает с уровня дохода 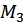и далее возрастает 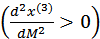. Графиком функции является выпуклая кривая III (рис. 2.11), про которую можно сказать, что с ростом дохода 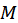она асимптотически приближается к прямой

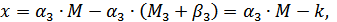
где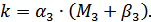

Следует отметить, что кривые спроса Торнквиста также можно получить при помощи решения задачи оптимального выбора, если использовать целевую функцию потребления в специальной степенной форме.

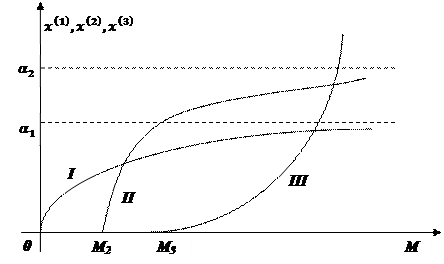Рис. 2.11. Графическое представление функций Торнквиста спроса на товары первой, второй необходимости и предметы роскоши.

Функции Торнквиста, однако, не дают полного представления закономерностей изменения спроса. Они не в полной мере отражают специфику движения спроса для различных групп товаров. В частности, они описывают только монотонное изменение спроса. Однако, для некоторых товаров существуют точки максимума (например, спрос на малоценные товары сначала возрастает, а затем – снижается) и точки перегиба (когда с ростом дохода 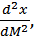положительна, а затем отрицательна: S - образная кривая).

Кроме того, трудно осуществить дифференциацию товаров на предметы первой необходимости, менее необходимые и предметы роскоши, тем более, что их состав меняется во времени. К тому же семьи с разным уровнем дохода различным образом определяют принадлежность товаров к указанным группам.

В зарубежной экономической теории существуют три концепции изменения потребления (спроса) под влиянием дохода, различающиеся трактовкой категории дохода как абсолютного, постоянного и относительного.

Первая из них принадлежит Дж. М. Кейнсу. В ней отражена тенденция сохранения потребителями потребления ресурсов во времени на стабильном уровне путем регулирования величины сбережений. Суммарный спрос и доход 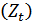делится на совокупные потребительские расходы 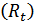, составляющие основную часть дохода, и сбережения 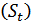: 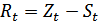. Отличительной особенностью концепции Кейнса является введение в рассмотрение величины, названной им склонностью к потреблению 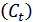и представляющей отношение потребительских расходов 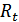к суммарному спросу :

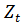На коротком промежутке времени t эта величина постоянна. В личных потребительских расходах также присутствует постоянная часть, равная 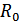. Таким образом, общий уровень личных потребительских расходов .

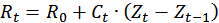Предельная склонность к потреблению 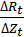положительна, при увеличении дохода она уменьшается, при уменьшении растет: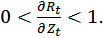

Такая закономерность проявляется как во временном разрезе — на протяжении экономического цикла, так и при переходе от групп населения с низкими доходами к группе с высокими доходами. В целом, с ростом дохода потребительские расходы растут, но медленнее, с падением дохода они сокращаются (также медленно). Поскольку склонность к потреблению принимается как постоянная функция абсолютного уровня дохода, эта концепция названа концепцией постоянного дохода.

В гипотезах относительного и постоянного (или перманентного) дохода величина потребительских расходов ставится в зависимость не от абсолютной, а от относительной или некой постоянной части дохода, не зависящей от времени.

Основой гипотезы относительного дохода, развитой Дж. Дьюзенберри, является утверждение, что расходы потребителя зависят не только от дохода, но и от социального положения в общей группе потребителей. На текущее поведение потребителя влияют решения других потребителей, близких к данному по социальному положению. Уровень полезности 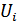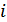-го потребителя является функцией вида:

где 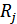– объем расходов потребителей 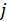- ой группы, 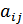– параметр, характеризующий уровень их влияния на поведение потребителя 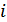- ой группы.

Таким образом, отличительной особенностью концепции относительного дохода является признание социальной взаимной обусловленности поведения потребителей. Влияние неравномерности распределения совокупных доходов на уровень расходов потребителей заключается в том, что с ростом дохода группы потребителей норма их потребительских расходов снижа­ется, и наоборот. Из теории относительного дохода также следует, что увеличение не­равенства доходов способствует повышению среднего уровня нормы накоплений и со­ответственно уменьшает долю потребительских расходов в доходах.

Представители концепции постоянного дохода (М. Фридман) считают, что потребительский спрос, являющийся результатом воздействия постоянных и случайных факторов[9], определяется не текущим, а усредненным доходом, который М. Фридман назвал перманентным Так, постоянный доход является той частью дохода, которая согласно ожиданиям потребителей сохранится в будущем. Временный доход – доход, который не ожидают сохранить в будущем.

Иными словами, постоянный доход является средним доходом, а временный доход - случайное отклонение от среднего значения. М. Фридман полагал, что потребление в основном зависит от постоянного дохода, поскольку потребители могут использовать свои сбережения для того, чтобы сгладить колебания во временном доходе.

В этом случае средняя склонность к потреблению зависит от отношения постоянного дохода к текущему доходу. Если текущий доход превышает постоянный, значение средней склонности к потреблению падает, напротив, если текущий доход меньше постоянного, средняя склонность к потреблению увеличивается.

Для полноты изложения рассмотрим также модель потребительского выбора Р. Стоуна, с помощью которой исследуют поведение потребителей с эластичным изменением спроса.

Пусть 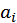- минимально необходимое количество блага 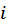- го вида, которое для 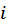- го потребителя не является предметом выбора. Параметры 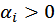характеризуют ценность блага 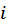- го вида для потребителя, 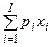- полная рыночная стоимость 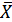- приобретаемого набора благ. Функция полезности Р. Стоуна может быть записана следующим образом:

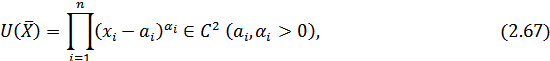
где 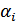- вес блага i-го вида в предпочтениях потребителя.

Экономический смысл коэффициентов весовой значимости состоит в том, что чем больше значение веса имеет благо, тем более предпочтительно оно для данного потребителя (или группы потребителей).

С учетом введенных обозначений модель Р. Стоуна имеет следующий вид:

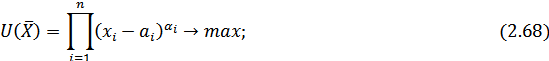
Для решения задачи потребительского выбора (2.68)-(2.70), являющейся задачей на условный экстремум с ограничениями в виде равенств, необходимо использовать условия оптимальности теоремы Куна-Таккера и составить функцию Лагранжа:

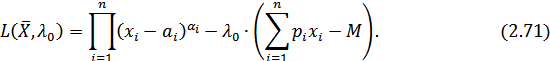
Определим первые частные производные функции Лагранжа (2.71) и построим систему уравнений, из которой найдем соотношения для объемов потребляемых производственных факторов 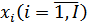, а также для множителя Лагранжа ():

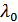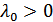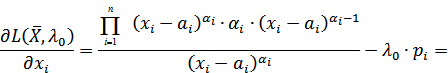
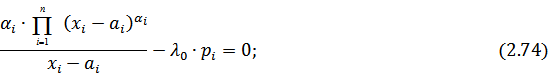
Рассмотрим возможный способ нахождения искомых величин. Исходя из (2.74), найдем значения :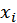

Из (2.76) с учетом (2.67) выразим 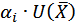, затем суммируем обе части равенства по i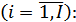

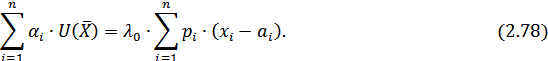
Из (2.78) с учетом ограничения (2.69) получим выражение для рассматриваемой функции полезности:

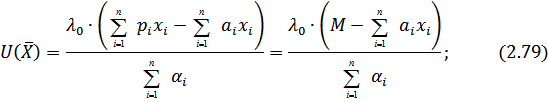
Определим функциональную зависимость объема потребляемого 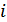- го блага от величины потребительского бюджета, цены блага, его относительного веса в системе потребительских предпочтений, а также нормы потребления:

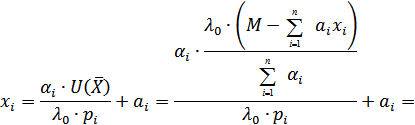
Сумма весов 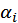по всему набору благ равна единице:

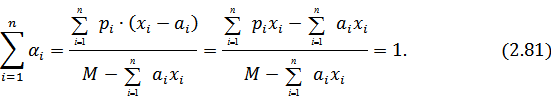
Функции спроса в модели Стоуна имеют следующую экономическую интерпретацию.

Вначале приобретается минимально необходимый объем каждого блага 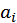, а затем оставшаяся часть дохода, равная

распределяется пропорционально «коэффициентам ценности» благ .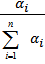

Разделив оставшиеся средства на цену 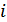-го блага, в которой учитывается «коэффициент его ценности», получим дополнительное его количество, при­обретаемое сверх минимума.

В частном случае, когда все то­вары имеют равную ценность для потребителя, функция спроса принимает вид:

Определим для этого случая эластичность спроса на 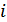- ый товар по цене j -го блага:

Полученный результат можно интерпретировать следующим образом: спрос на 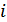- ый товар не зависит от цены 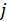-го блага и имеет тенденцию к уменьшению при увеличении его цены 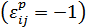. Таким образом, можно утверждать, что в модели Р. Стоуна каждый товар является нормальным и ценным.

Определим эластичность спроса на 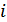- ый товар по бюджету:

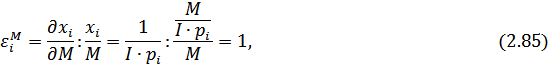
то есть спрос на 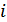- ое благо при увеличении дохода растет с эластичностью, равной 1: каждое благо является «предметом роскоши».

В рассмотренных выше постановках задачи потребительского выбора существенную роль играют цены, выступающие регуляторами спроса. Однако такой подход справедлив лишь в том случае, когда цены являются достаточно гибкими: время их изменения сравнимо с длительностью основных производственных циклов.

Во многих случаях реалистичной оказывается ситуация, когда изменение цен происходит медленнее, чем изменяются параметры производственных процессов. В этом случае цены не могут непосредственно регулировать спрос.

В настоящее время активно развивается подход к описанию таких процессов, в которых роль регулирующих параметров признается за величинами, представляющими отношение спроса и предложения.

Введем показатель отношения спроса к предложению по 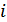-му благу:

где 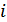- индекс товара, 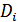– потребительский спрос, 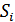- предложение товара со стороны производственной сферы.

В измененной постановке задачи оптимального выбора в качестве искомых выступают объемы потребления благ не в натуральном, а в стоимостном выражении. Таким образом, компоненты потребительского набора 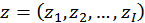- объемы потребления в текущих ценах, которые, как уже отмечено выше, изменяются медленно.

В этом случае бюджетное ограничение принимает вид:

а в выражение функции потребительского предпочтения явным образом вводятся введенные выше параметры: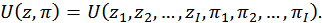

Задача потребительского выбора имеет вид:

где 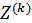- множество допустимых потребительских наборов в стоимостном выражении.

Очевидно, неравенство 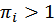соответствует ситуации, когда спрос на товар 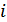-ой группы превышает его предложение, т.е. имеется дефицит товара в системе «спрос-предложение»; если же 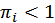, то товар 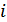-го вида вполне доступен для потребителя и его предложение превосходит спрос.

При помощи использования корректировочных показателей в целевой функции потребления удается уравнять предпочтения потребителей по отношению к дефицитным и, наоборот, более доступным товарам. В частности, если исходить из взаимозаменяемости товарных групп, то можно воспользоваться функцией предпочтения в виде

Здесь при помощи показателей 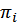уравниваются возможности получения дефицитных и доступных товаров, поскольку в выражении функции потребительского предпочтения участвует нормированный объем товара.