Соотношение (2.18) позволяет утверждать, что предельная полезность денежной ед. потребителей с разным уровнем бюджета 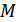 различна. Докажем, что с ростом бюджета
различна. Докажем, что с ростом бюджета 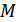 предельная полезность денег падает, а при его сокращении – растет.
предельная полезность денег падает, а при его сокращении – растет.
Приведем доказательство этого факта для случая набора из двух благ.
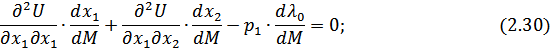
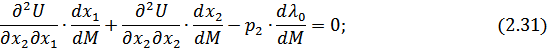

Для удобства обозначим смешанные производные функции 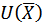 в точке
в точке 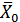 символом
символом 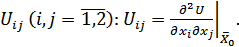
Представим систему уравнений (2.30) – (2.32) в матричной форме:
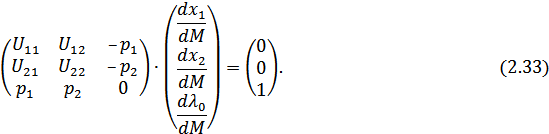
Система (2.33), состоящая из трех уравнений с неизвестными 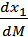 ,
, 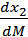 ,
, 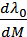 по теореме Крамера является определенной и имеет единственное решение в том случае, если определитель матрицы системы (2.33) не равен нулю.
по теореме Крамера является определенной и имеет единственное решение в том случае, если определитель матрицы системы (2.33) не равен нулю.
Покажем, что определитель матрицы системы (2.33) отличен от нуля. Вычислим алгебраическую сумму всех правильных произведений матрицы:
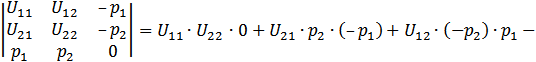
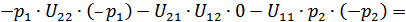
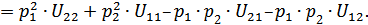
В силу соотношения (2.19) и совпадения смешанных частных производных 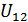 и
и 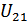 функции
функции 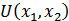 упростим полученное выражение:
упростим полученное выражение:
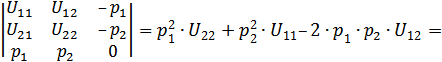
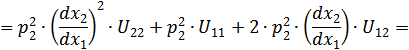

Убедимся, что выражение, стоящее в скобках, является вторым дифференциалом функции 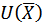 :
:
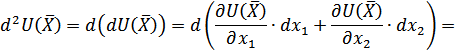
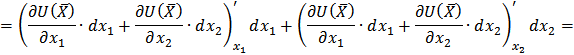
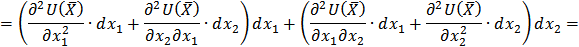
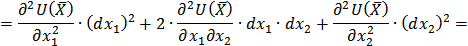
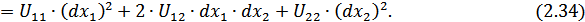
Т. к. точка 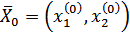 является точкой локального максимума функции
является точкой локального максимума функции 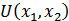 , то в силу критерия Сильвестра значение ее второго дифференциала в этой точке меньше нуля:
, то в силу критерия Сильвестра значение ее второго дифференциала в этой точке меньше нуля: 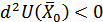 . Кроме того, отношение
. Кроме того, отношение 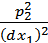 в силу предположения о положительности рыночных цен больше нуля.
в силу предположения о положительности рыночных цен больше нуля.
Таким образом, определитель матрицы системы уравнений (2.33) строго меньше нуля.
Доказанный факт позволяет по формуле Крамера найти значение 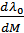 в точке
в точке 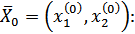
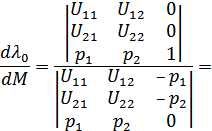
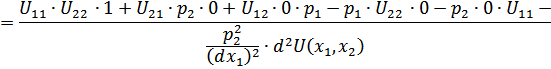
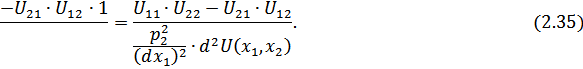
Поскольку 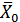 - точка локального максимума функции
- точка локального максимума функции 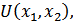 то, согласно критерию Сильвестра, алгебраическая сумма правильных произведений
то, согласно критерию Сильвестра, алгебраическая сумма правильных произведений 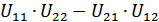 должна быть больше нуля.
должна быть больше нуля.
Следовательно, значение выражения, стоящего в числителе, будет больше нуля, а выражения, стоящего в знаменателе – меньше нуля.
Таким образом, доказано, что в точке оптимума 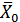 задачи потребительского выбора предельная полезность денег обратно зависит от величины бюджета
задачи потребительского выбора предельная полезность денег обратно зависит от величины бюджета 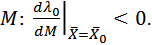
 2015-05-10
2015-05-10 506
506








