Рассмотрим ситуацию, когда в результате неблагоприятного изменения условий рыночной конъюнктуры, повлекших повышение цен на одно или несколько благ, потребителю, с целью сохранения достигнутого за предыдущие интервалы времени уровня потребительской полезности, необходимо определить денежную компенсацию к первоначальному бюджету. Предполагается, что потребитель полностью осведомлен о состоянии своих потребительских предпочтений и выборов, осуществленных на предыдущих временных интервалах.
Как и в модели (2.11), (2.12’), (2.13) допустим, что предпочтения потребителя описываются априорно заданной СФПП 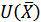 ,
, 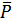 и
и 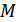 - вектор рыночных цен на приобретаемые блага и размер бюджета потребителя соответственно. Тогда
- вектор рыночных цен на приобретаемые блага и размер бюджета потребителя соответственно. Тогда 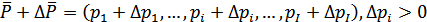 - новый вектор цен,соответствующий изменившимся рыночным условиям.
- новый вектор цен,соответствующий изменившимся рыночным условиям.
Таким образом, необходимо определить минимальный размер дополнительной компенсации 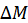 , на величину которой требуется увеличить первоначальный бюджет потребителя
, на величину которой требуется увеличить первоначальный бюджет потребителя 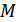 с целью сохранения его достигнутой ранее потребительской полезности, соответствующей изокванте
с целью сохранения его достигнутой ранее потребительской полезности, соответствующей изокванте 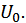
Cформулируем математическую постановку задачи определения компенсированного бюджета потребителя:





Модель (2.49)-(2.53) является задачей на условной экстремум с ограничениями в виде неравенств и функционалом на минимум. Для того, чтобы использовать необходимые условия оптимальности теоремы Куна-Таккера, требуется показать, что функционал (2.49) и система ограничений (2.50)-(2.53) являются выпуклыми на Ω функциями.
Функционал 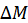 задачи (2.49)-(2.53) (выражение (2.49)) является линейной функцией одной переменной, а, следовательно,
задачи (2.49)-(2.53) (выражение (2.49)) является линейной функцией одной переменной, а, следовательно, 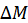 - выпуклая функция.
- выпуклая функция.
Аналогично, 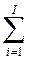
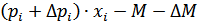 также является выпуклой в экономической области потребителя.
также является выпуклой в экономической области потребителя.
Наконец, поскольку, согласно условию (2.5), СФПП 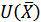 на Ω является вогнутой по каждому аргументу, то
на Ω является вогнутой по каждому аргументу, то 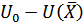 - выпуклая на Ω функция.
- выпуклая на Ω функция.
Кроме того, в экономической области потребителя всегда найдется такой набор благ 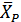 и такое
и такое 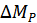 , для которых справедливы следующие условия:
, для которых справедливы следующие условия:

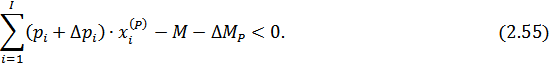
Следовательно, установлено, что экономическая область Ω потребителя удовлетворяет условию Слейтера, что позволяет построить функцию Лагранжа модели (2.49)-(2.53):
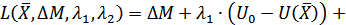
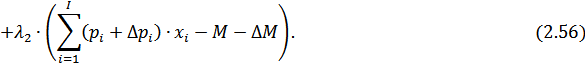
Используем условия оптимальности теоремы Куна-Таккера:
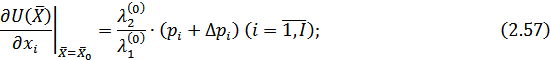

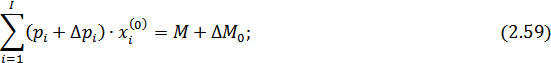


где 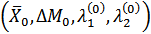 - решение системы уравнений (2.57) - (2.61).
- решение системы уравнений (2.57) - (2.61).
Условия оптимальности (2.57)-(2.61) решения модели компенсированного бюджета потребителя (2.48)-(2.52) позволяют установить экономическое содержание множителей Лагранжа 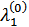 и
и 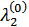 .
.
Так, множитель Лагранжа 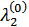 , являющийся двойственной оценкой бюджетного ограничения (2.50), показывает величину, на которую снизится объем компенсации потребителю в случае, если его первоначальный бюджет увеличится на одну денежную ед. Этот результат вполне ожидаем: каждая дополнительная ед. собственных средств потребителя вытесняет некоторый объем дополнительных средств, авансируемых на покупку товара.
, являющийся двойственной оценкой бюджетного ограничения (2.50), показывает величину, на которую снизится объем компенсации потребителю в случае, если его первоначальный бюджет увеличится на одну денежную ед. Этот результат вполне ожидаем: каждая дополнительная ед. собственных средств потребителя вытесняет некоторый объем дополнительных средств, авансируемых на покупку товара.
Множитель 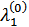 (двойственная оценка ограничения (2.49) в точке
(двойственная оценка ограничения (2.49) в точке 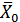 ) характеризует рыночную цену набора благ, приходящуюся на ед. его предельной полезности, и, как следует из свойств оптимального решения модели потребительского выбора, является постоянной для всех благ из набора
) характеризует рыночную цену набора благ, приходящуюся на ед. его предельной полезности, и, как следует из свойств оптимального решения модели потребительского выбора, является постоянной для всех благ из набора 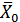 . Более того, увеличение минимальной общей полезности
. Более того, увеличение минимальной общей полезности 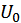 на одну ед. ведет к увеличению объема
на одну ед. ведет к увеличению объема 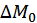 дополнительно привлекаемых потребителем бюджетных средств на величину двойственной оценки
дополнительно привлекаемых потребителем бюджетных средств на величину двойственной оценки 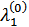 .
.
 2015-05-10
2015-05-10 631
631








