Основные свойства обратной связи

Лабораторная работа №7

Исследование свойств обратной связи (динамический режим).

1.Цель работы является:

изучить свойста обратной связи в функции частоты;

получить навыки в задании и определении области устойчивости;

изучить свойства интеграла обратной связи;

получить навыки, позволяющие преобразовывать излишние запасы по фазе в увеличение глубины обратной связи в требуемом диапазоне частот.

Основные свойства обратной связи.

Свойства обратной связи рассмотрим на примере одноконтурной системы регулирования (рис.1).

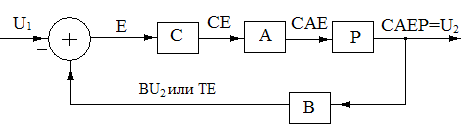
Рис.1 Структурная схема одноконтурной системы регулирования (С – регулятор; А – усилитель мощности; Р – объект регулирования; В – датчик обратной связи).

Динамические свойства системы регулирования описываются передаточными функциями замкнутых систем по управлению

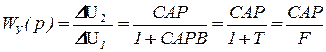(1)

и по ошибке

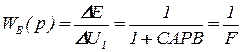(2)

где Δ 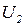, ∆ 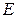- приращение выходных сигналов; ∆ 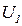- приращение входного сигнала; 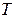– передаточная функция петли или возвратное отношение; 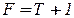– возвратная разность; | 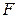| - глубина обратной связи.

Исследуем свойства обратной связи, анализируя выражения (1) и (2). Так как передаточная функция разомкнутой системы (передаточная функция петли или возвратное отношение 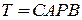) величина векторная, зависящая от частоты, то знаменатель выражений (1) и (2) 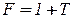может принимать значения больше единицы ( 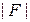>1) или меньше единицы ( 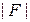<1). При 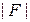>1 обратная связь отрицательная, при 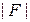<1- положительная. Является ли обратная связь положительной или отрицательной, зависит от амплитуды и фазы сигнала обратной связи (возвратного отношения), а не только от знака у сумматора обратной связи, как это довольно часто утверждается в учебниках по теории автоматического управления. Это можно проиллюстрировать, рассмотрев векторные диаграммы сигналов 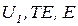, характеризующие сумматор (рис.2).

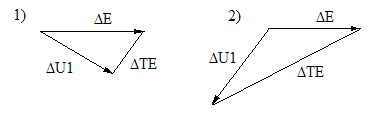
Рис 2. Векторные диаграммы сигналов сумматора: 1) – положительная обратная связь; 2) – отрицательная обратная связь.

Из рис 2.1 видно, что ∆ 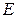>∆ 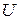1, т.е. сигнал на выходе больше, чем на входе. Так как приращение входного сигнала увеличивает приращение ошибки, то такая связь является положительной. При других соотношениях сигналов (сигналы определены на других частотах) ∆ 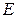< ∆ 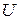1 (рис. 2.2) обратная связь является «отрицательной». Так как передаточная функция разомкнутой системы 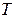зависит от частоты, то обратная связь последовательно проходит несколько этапов. 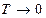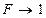При низких частотах, как правило, обратная связь отрицательна, в районе частоты среза она становится положительной, а затем, на более высоких частотах, когда , a и 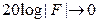, обратная связь становится незначительной.

Проиллюстрируем вышеизложенные положения несколькими примерами.

Пример 1.

Коэффициент усиления прямой цепи (прямой передачи) 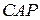=100, а коэффициент обратной связи 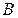=-0.003. Передаточная функция разомкнутой системы (возвратное отношение) равно 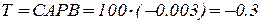. Возвратная разность равна 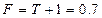, т.е. обратная связь положительная. Представляя полученные знания в (1), имеем:

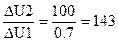
Так как выходной сигнал в замкнутой системе больше, чем в разомкнутой системе (143>100), то обратная связь положительная.

Как на входе элемента сравнения появился минус, и как комбинация входных сигналов блока сравнения дала положительную обратную связь можно установить, используя, для наглядности, частный случай представления векторное представление сигналов. Подадим на вход системы 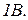, а на выходе системы, при некоторой частоте, получим 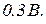Кроме того потребуем, чтобы сигнал на выходе системы отставал от входного сигнала на 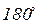градусов. При таком соотношении входного и выходного сигналов возвратная разность стала меньше еденицы, что и привело к положительной обратной связи. В этом примере, для наглядности математических преобразований, было принято, чтобы выходной сигнал отставал от входного сигнала на 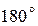градусов. Тогда векторное и алгебраическое суммирование дают одинаковый результат, так как вектора лежат на одной прямой.

Объясним это явление с физических позиций. Предположим, что на вход системы подан гармонический сигнал с частотой 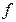, на входе сумматора появился сигнал обратной связи той же частоты, сдвинутый по фазе на 180. В сумматоре этот сигнал инвертируется (меняет фазу на 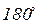градусов), т. е. совпадает с входным сигналом. Следовательно, сигнал на выходе сумматора будет больше, чем на его входе, т. е. появилась положительная обратная связь.

Таким образом, в расчетах должно использоваться векторное представление сигналов, поступающих на сумматор.

Пример 2.

Пусть коэффициент усиления петли прямой передачи остался прежним 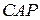=100, а у коэффициента обратной связи изменился знак: 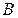=0.003. Тогда 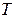=0.3, а 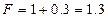. При 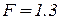обратная связь отрицательная, так как выходной сигнал в замкнутой системе меньше, чем в разомкнутой системе (77<100).

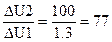
Для того, чтобы векторное сложение и скалярное совпадали, необходимо ввести ограничения на аргумент вектора 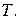Можно, например, потребовать, чтобы аргумент вектора 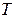был равен 360 градусов или определять аргумент вектора 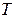, используя его проекцию на действительную ось.

Из примеров следует, когда | 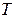| мало (| 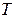|<1), знак 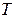однозначно определяет, является ли обратная связь положительной или отрицательной. Когда | 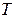|>2, то обратная связь отрицательна, т.е. когда модуль передаточной функции разомкнутой системы возрастает. Это, как правило, имеет место при уменьшении частоты.

Проиллюстрируем вышеизложенные положения на конкретном примере передаточной функции разомкнутой системы:

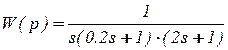(3)

По передаточной функции (3) в пакете Control System Toolbox построена логарифмическая характеристика (рис.3) и АФХ разомкнутой системы (рис.4).

Программа 1 bod_01.m

h1=tf(0.1,[1,0]); %Передаточная функция интегратора.

h2=tf(1,[0.2,1]); %Передаточная функция апериодического звена.

h3=tf(10,[2,1]); %Передаточная функция апериодического звена.

h=h1*h2*h3; %Передаточная функция трех звеньев.

h=h1*h2*h3;