По сетке Вульфа

Положим перед собой сетку Вульфа так, как это показано на рис. 6.

Далее, будем иметь в виду, что никакие построения на самой сетке не производятся - задачи целиком решаются на листке кальки, наложенном на сетку.

Чтобы иметь возможность всегда приводить кальку относительно сетки в одно и то же исходное положение, отмечаем на кальке центр сетки точкой с четырьмя черточками в виде креста, не доходящими до самой точки. Кроме того, у правого конца горизонтального диаметра сетки ставится небольшая черточка, проведённая вне круга проекций (рис.9).

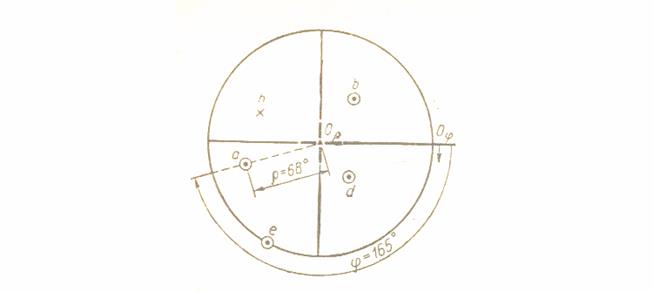
Рис. 12. Построение на кальке по сетке Вульфа к задачам 1 и 2.

Черточка справа будет служить нулевым индексом для долгот 0 φ, а центральная точка рисунка – местом нуля для полярных расстояний 0 ρ. Первая сферическая координата – долгота φ – отсчитывается по кругу проекций от нулевого индекса по часовой стрелке (на сетке каждое деление соответствует 2^о, каждый десятый градус выделен жирной линией). Вторая сферическая координата – полярное расстояние ρ – отсчитывается от центра сетки.
Необходимо условиться, что в дальнейшем изображённые на сетке дуги меридианов и параллелей будут служить вспомогательными линиями. Истинный полюс сетки находится в ее центре 0 ρ, истинный экватор совпадает с кругом проекций, а из истинных меридианов на сетке изображены только два – вертикальный и горизонтальный диаметры сетки. При работе с сеткой Вульфа необходимо мысленно представлять себе совмещённую с ней простейшую стереографическую сетку (рис. 9). Отсчёт полярных расстояний ρ должен производиться при этом от центра сетки как от полюса.

Задача 1. Построить стереографическую проекцию направления, заданного сферическими координатами ρ и φ.

Пусть некоторое направление А задано сферическими координатами φ =165^о и ρ =68^о: А (165^о, 68^о). Найти стереографическую проекцию этого направления.
Для решения задачи:

1) накладываем кальку на сетку и ставим на ней центральный крестик и черточку нулевого индекса для φ;

2) от нулевого индекса для φ по кругу проекций (по часовой стрелке) отсчитываем первую сферическую координату – долготу φ (165^о) и отмечаем результат на внешнем круге вспомогательной точкой (рис.12);

3) вращением кальки (центр кальки при этом всегда должен совпадать с центром сетки) совмещаем найденную вспомогательную точку с концом ближайшего диаметра сетки;

4) по этому диаметру от центра сетки в сторону вспомогательной точки отсчитываем вторую сферическую координату – полярное расстояние ρ (68^о) – и отмечаем найденную точку небольшим кружком;

5) возвращаем кальку в исходное положение и надписываем точку а. Точка а является искомой стереографической проекцией направления А.

В кристаллографии эта задача применяется при решении вопросов:

1. Даны сферические координаты нормали к грани кристалла; требуется найти стереографическую проекцию нормали к грани.

2. Даны сферические координаты ребра кристалла или его характерного направления (например, оси симметрии); требуется построить стереографическую проекцию этого ребра (или направления).Предлагаем изобразить стереографические проекции следующих направлений:
В (309^о, 55^о), D (51^о, 37^о), Е (122^о, 90^о) и Н (205^о, 124^о).

Задача 2 (обратная). Определить сферические координаты направления, заданного стереографической проекцией.

1. Вращением кальки приводим заданную точку (стереографическую проекцию направления) на ближайший диаметр сетки. По этому диаметру от центра сетки до заданной точки отсчитываем сферическую координату ρ и отмечаем вспомогательной точкой на круге проекций тот конец диаметра, в направлении которого лежит наша точка.

2.Приводим кальку в исходное положение и по кругу проекций отсчитываем сферическую координату φ от нулевого индекса по часовой стрелке до вспомогательной точки.

Задача 3. Провести дугу большого круга через заданные стереографические проекции двух направлений.

Например, провести дугу большого круга через стереографические проекции а и в направлений А (165^о, 68^о) и В (309^о, 55^о).

1.Вращением кальки добиваемся того, чтобы обе заданные точки а и в оказались на одной из вспомогательных меридиональных дуг сетки Вульфа.

2.Найденную дугу тщательно обводим карандашом и возвращаем кальку в исходное положение (рис.13).

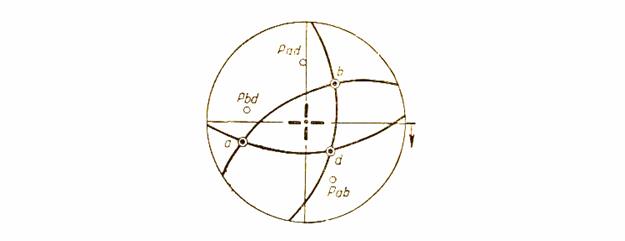
Рис. 13. Построение стереографических проекций к задачам 3,4,5,6 и 7.

Если заданные точки изображают стереографические проекции рёбер, то найденная дуга большого круга является стереографической проекцией грани, в плоскости которой лежат эти рёбра. Предлагаем провести на кальке дуги в d и а d через заданные точки.

Задача 4. Измерить угол между двумя направлениями, заданными их стереографическими проекциями (например, угол между направлениями А и В).

1.Вращением кальки совмещаем данные точки а и в с одной из меридиональных дуг сетки Вульфа (задача 3).

2. Отсчитываем по этой меридиональной дуге количество градусов, заключённых между точками а и в (рис.13). В результате получаем угол АВ=113^о. Если заданные точки представляют собой гномостереографические проекции граней, то измеренный угол является углом между нормалями к этим граням. Если же заданные точки являются стереографическими проекциями рёбер, то измеренный угол есть угол между этими рёбрами.

Задача 5. Найти полюс дуги большого круга, заданной на стереографической проекции (под полюсом дуги принимают точку, равноотстоящую от всех точек дуги на 90^о).

Например, требуется найти полюс дуги а в (рис.13).

1.Вращением кальки совмещаем заданную дугу а в с соответствующей меридиональной дугой сетки Вульфа.

2.Отсчитываем по горизонтальному диаметру сетки от точки пересечения заданной дуги с этим диаметром по направлению к центру сетки 90^о(перейдя за него) и отмечаем кружком найденную точку.

3.Вращаем кальку в исходное положение и надписываем точку – Р _ав. Найденная точка Р _ав, как легко проверить, действительно является полюсом дуги а в.

Если заданная дуга представляет собой стереографическую проекцию грани, то найденный полюс дуги является стереографической проекцией направления, перпендикулярного к этой грани, или, что то же самое, гномостереографической проекцией самой грани.

Если заданная дуга является гномостереографической проекцией ребра, то полюс дуги представляет собой стереографическую проекцию того же ребра. Предлагаем найти полюса дуг ав, вd, и аd и определить их сферические координаты. Ответы: Р _ав (62^о, 61^о); Р _вd (194^о, 59^о); Р _аd (269^о, 60^о).

Задача 6 (обратная). По заданному полюсу найти дугу большого круга, отвечающую его экватору.

1.Вращением кальки приводим заданный полюс на горизонтальный диаметр сетки.

2.Отсчитываем по горизонтальному диаметру в направлении центра сетки 90^о (перейдя за него) и обводим проходящую здесь меридиональную дугу. Эта последняя будет искомой экваториальной дугой относительно заданного полюса.

Если заданный полюс выражает гномостереографическую проекцию грани, то найденная экваториальная дуга соответствует стереографической проекции той же грани.

Если заданный полюс представляет стереографическую проекцию ребра, то найденная дуга отвечает его гномостереографической проекции. Обратите внимание на решение задач 5 и 6, так как они содержат механизм переходов от стереографической проекции к гномостереографической и обратно.

Задача 7. Измерить угол между двумя дугами больших кругов.

Например, требуется измерить угол между дугами ав и аd (рис.10).1.Вращением кальки совмещаем точку пересечения дуг – а (вершину измеряемого угла) с горизонтальным диаметром сетки. 2. Приняв эту вершину за полюс, приводим отвечающую ему экваториальную дугу (задача 6).3.Количество градусов, заключённое в этой дуге между точками пересечения с ней двух заданных дуг, и является величиной искомого угла.

Если заданные дуги больших кругов являются стереографическими проекциями граней, то измеренный угол представляет собой угол между гранями при вершине а равен 65^о, при вершине в – 75^о и при вершине d – 116^о.

Задача 8. Построить геометрическое место точек, образующих с заданной на проекции точкой одно и то же угловое расстояние α (задача на построение малого круга).

Вокруг некоторого направления, стереографическая проекция которого отвечает заданной на проекции точке, имеется множество направлений, отклонённых от первого на один и тот же угол α и образующих в совокупности конус с углом раствора 2 α. Пересечение этого конуса с поверхностью сферы даёт малый круг, в центре которого находится точка пересечения заданного направления со сферой. Стереографическая проекция исходного направления является только стереографическим, а не геометрическим центром (геометрический центр совпадает со стереографическим только в том частном случае, когда это направление совмещено с осью проекций). В этом основная трудность задачи. Пусть заданная точка лежит внутри круга проекций (например, точка в (309^о, 55^о). Требуется построить вокруг нее как стереографического центра малый круг заданного радиуса (на рис. 12 α = 30^о).

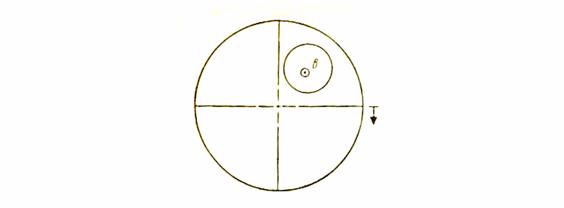
Рис.14. Построение вокруг стереографического центра.

малого круга заданного радиуса к задаче 8

Для этого совмещаем заданную точку с какой-либо параллелью, изображённой на сетке Вульфа, отсчитываем по меридиональной дуге сетки, проходящей через исходную точку, вверх и вниз угловое расстояние α и отмечаем полученные при этом две точки. Вращением кальки приводим заданную точку на какую-либо другую параллель сетки и снова аналогичным путём получаем пару новых точек. Повторяем такой приём до тех пор, пока полученные точки не начнут совершенно отчётливо обрисовывать окружность. Эта последняя может быть вычерчена с помощью одной из параллелей сетки Вульфа, кривизна которой соответствует искомому кругу. Для этого центр кальки сдвигается с центра сетки, и часть построенных точек совмещается путём наложения с параллелью, приёмов вычерчивается требуемый малый круг. Решение задачи упрощается при наличии циркуля.

Поворотом кальки приводим заданную точку на горизонтальный диаметр сетки и отсчитываем вправо и влево от нее требуемый угол α. Взяв геометрическую середину найденного отрезка, принимаем ее за центр и вычерчиваем требуемый круг. Если исходная точка лежит слишком близко к кругу проекций – задача решается по трём точкам, из которых две берутся по соответствующему меридиану сетки. В частном случае, когда заданная точка лежит на внешнем круге проекций (ρ =90^о), достаточно привести ее поворотом кальки на один из полюсов, изображённых на сетке Вульфа, отсчитать в любую сторону по кругу (или по любой вспомогательной меридиональной дуге сетки) требуемый угол и прочертить соответствующую параллель сетки. В случае совпадения заданной точки с центром проекций отсчитываем по обоим диаметрам сетки угловые расстояния α и по четырём найденным точкам строим искомую окружность. Построение малых кругов широко используется при решении задач, когда по двум заданным точкам и по углам между ними и третьей искомой точкой требуется изобразить эту последнюю (задача 10).

Задача 9. Даны измеренные на гониометре сферические координаты граней кристалла:

Таблица 6

Грани φ,град. ρ,град.

-

Требуется: 1)изобразить гномостереографические и стереографические проекции всех граней (задачи 1 и 6);

2)измерить углы между гранями (задачи 4 и 7);

3)изобразить гномостереогрфические и стереографические проекции рёбер (задачи 3 и 5);

4)найти сферические координаты рёбер и измерить углы между рёбрами (задачи 2, 4 и 7).

Задача 10. Построить гномостереографическую проекцию кристалла по углам между нормалями к граням (именно такие углы, измеряются на отражательном гониометре). Они легко находятся посредством прикладного гониометра).Даны углы между нормалями к граням (рис.15):

В:С=83^о В:Р=42^о Р:С=72^оР:Q=54^о
В ^/:О=58^о В:В ^/ =180^о С:О=54^о

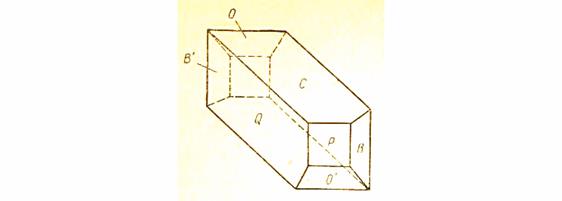
Рис. 15. Построение гномостереографической проекции кристалла

по углам между нормалями к граням (к задаче 10).

Для проектирования данного кристалла придаем ему такую пространственную ориентировку, при которой грани В, Р, Q и В ^/ становятся вертикальными и изобразятся на внешнем круге проекций. Проекцию одной из этих граней, например, грани В, совместим с нулевым индексом для φ. В соответствии с рисунком кристалла отсчитываем по часовой стрелке углы между нормалями к граням В:Р=42^о, Р:Q=54^о и В:В ^/ =180^о. Найденные на внешнем круге точки и будут проекциями этих вертикальных граней. Далее по углам В: С = 83^о и Р: С = 72^онаходим точку С. Для этого приводим сначала точку В в один из полюсов сетки Вульфа, отсчитываем по кругу проекций в любую сторону 83^о и прочерчиваем соответствующую параллель сетки. Затем совмещаем с полюсом сетки точку Р, отсчитываем 72^о и снова прочерчиваем параллель сетки. На пересечении двух полученных параллелей и находится проекция грани С (задача 8). Для нахождения проекции грани О совмещаем точку В ^/ с одним из изображённых полюсов сетки, отсчитываем 58^о и рисуем параллель. Далее принимаем за стереографический центр точку С и строим малый круг, радиусом и 54^о (задача 8). Этот круг пересекает параллель, вычерченную вокруг В ^/ в двух точках. В соответствии с рисунком, принимаем за проекцию грани О, которая соответствует расположению грани на рисунке. Дополнительно следующие вопросы:

1.Определить сферические координаты граней В, Р, Q, В ^/, С, О (задача 2).

2.Измерить угол между нормалями к граням С и О (задача 4).

3.Найти стереографические проекции рёбер СВ и СР и определить их сферические координаты (задачи 3, 5, 2).

4.Построить стереографическую проекцию грани О (задача 6).