Для тройных интегралов, как и для двойных, имеют место формулы замены переменных при переходе от прямоугольных координат к новым системам координат, наиболее употребительными из которых являются цилиндрические и сферические координаты.
Переход от прямоугольных координат 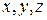 к цилиндрическим координатам
к цилиндрическим координатам 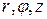 (рис. 6.8), связанным с
(рис. 6.8), связанным с 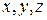 соотношениями
соотношениями
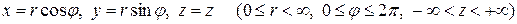 ,
,
осуществляется по формуле
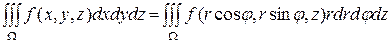 .
.
Выражение 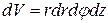 называют элементом объема в цилиндрических координатах.
называют элементом объема в цилиндрических координатах.
Название «цилиндрические координаты» связано с тем, что координатная поверхность 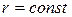 (т.е. поверхность, все точки которой имеют одну и ту же координату r) является цилиндром, прямолинейные образующие которого параллельны оси
(т.е. поверхность, все точки которой имеют одну и ту же координату r) является цилиндром, прямолинейные образующие которого параллельны оси 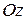 .
.
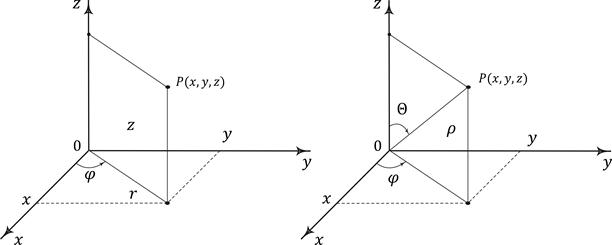
Рис. 6.8. Цилиндрические (слева) и сферические (справа) координаты
Переход от прямоугольных координат 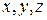 к сферическим координатам
к сферическим координатам 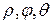 (рис. 6.8), связанным с
(рис. 6.8), связанным с 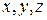 соотношениями
соотношениями
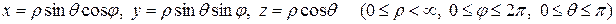 ,
,
осуществляется по формуле
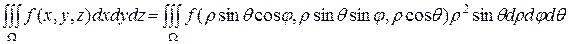 .
.
Выражение 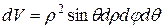 называют элементом объема в сферических координатах.
называют элементом объема в сферических координатах.
Название «сферические координаты» связано с тем, что координатная поверхность 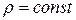 (т.е. поверхность, все точки которой имеют одну и ту же координату
(т.е. поверхность, все точки которой имеют одну и ту же координату 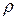 ) является сферой с центром в начале координат.
) является сферой с центром в начале координат.
Пример. Вычислить тройной интеграл
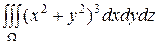 ,
,
где 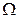 – область, ограниченная поверхностями
– область, ограниченная поверхностями 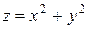 и
и 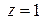 (рис. 6.9).
(рис. 6.9).
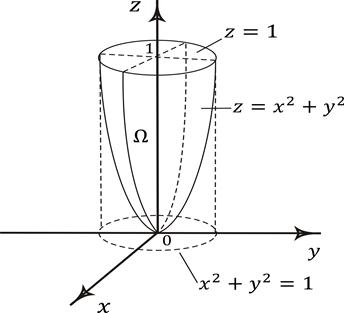
Рис. 6.9. Пример вычисления тройного интеграла в цилиндрических координатах
В данном примере удобно перейти от прямоугольных к цилиндрическим координатам.
Так как область 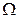 проектируется на плоскость
проектируется на плоскость 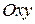 в круг
в круг 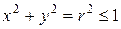 , то угол
, то угол 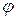 изменяется в пределах от 0 до
изменяется в пределах от 0 до 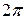 , радиус-вектор r изменяется в пределах от 0 до 1. Координата z изменяется от значений для точек, лежащих на параболоиде
, радиус-вектор r изменяется в пределах от 0 до 1. Координата z изменяется от значений для точек, лежащих на параболоиде 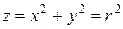 , до значений для точек, лежащих на плоскости
, до значений для точек, лежащих на плоскости 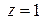 , т.е.
, т.е. 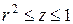 .
.
Применяя формулу для вычисления тройного интеграла в цилиндрических координатах, получаем
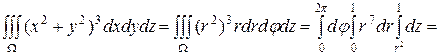

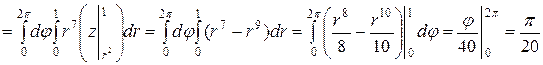 .
.
 2015-04-23
2015-04-23 8242
8242








