Расчет прочности по наклонным сечениям на действие изгибающего момента

Расчет выполняется из условия:

,

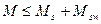где М – момент в наклонном сечении с длиной проекции с от внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения;

M_s – момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение;

М_sw – момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение.

,

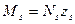где 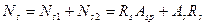- усилие в продольной растянутой арматуре. Если наклонное сечение пересекает А_sp без анкеров в пределах длины ее зоны анкеровки l_an, то

,

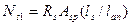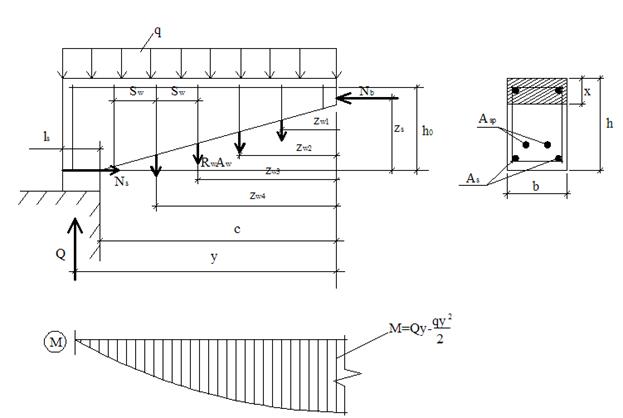Рис 2.12 К расчету по наклонным сечениям на действие изгибающего момента

где l_s – смотри рис. 2.12;

l_an – смотри ниже.

При наличии анкеров арматуры у A_s

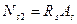
При отсутствии у арматуры A_s анкеров

,

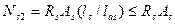где l_as – длина зоны анкеровки ненапрягаемой арматуры, определяемая по формуле (2.29).

При приварке к A_s поперечной или распределительной арматуры N_s2 увеличивается на величину N_w, определяемую по формулам пособий.

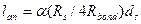, (2.29)

где 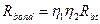- расчетное сопротивление сцепления арматуры с бетоном, 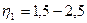- коэффициент, учитывающий влияние поверхности арматуры (зависит от профиля и диаметра арматуры. Так, для гладкой арматуры класса А240 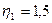, для арматуры классов А300-А1000 );

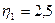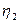- коэффициент, учитывающий влияние диаметра арматуры принимаемый равным:

1,0 – при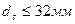

0,9 – при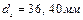

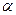- коэффициент, учитывающий влияние поперечного обжатия бетона и поперечной арматуры, принимаемый равным:

а) для крайних свободных опор балок

- при ;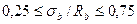

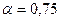- пр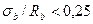и и ;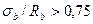

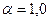где ;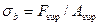

F_sup, A_sup - опорная реакция и площадь опирания балки.

При наличии поперечной арматуры, охватывающей без приварки продольную арматуру, коэффициент 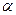делится на величину 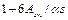(где A_sw и s – площадь сечения огибающего хомута и его шаг) и принимается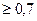

б) для свободных концов консолей 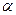=1

В любом случае принимается ;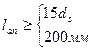

z_s – плечо внутренней пары сил, определяемое по формуле

,

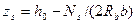но при наличии 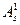(без 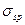) 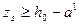. Допускается принимать z_s=0,9h₀.

M_sw определяется по формуле ,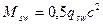

где q_sw – по формуле (2.31), а с по формуле (2.30)

Определение с

Для свободно опертых балок при равномерно распределенной нагрузке невыгоднейшее наклонное сечение начинается от грани опоры и имеет проекцию с, равную

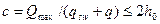, (2.30)

где 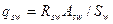(2.31)